题目内容
19.袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为$\frac{1}{7}$,现有甲、乙两人从袋中轮流摸取1球.甲先取,乙后取,然后甲再取…取后不放回,每人最多取两次,若两人中有一人首先取到白球时则终止,每个球在每一次被取出的机会是等可能的.(1)求袋中原有白球的个数;
(2)求甲取到白球的概率;
(3)求取球4次终止的概率.
分析 (1)设袋中原有n个白球,利用等可能事件概率计算公式能求出袋中原有3个白球.
(2)甲只有可能在第1次和第3次取球,记“甲第一次取到白球”的事件为A1,“第3球取到白球”的事件为A3,由事件A1,A3两两互斥,能求出甲取到白球的概率.
(3)因为第四次轮到乙取球,“第四次乙取到白球”的事件为B,“第四次乙取不到白球”的事件为C,由此能求出取球4次终止的概率.
解答 解:(1)设袋中原有n个白球,
由题意知:$\frac{1}{7}=\frac{C_n^2}{C_7^2}=\frac{{\frac{n(n-1)}{2}}}{{\frac{7×6}{2}}}$,解得n=3,
即袋中原有3个白球.…(4分)
(2)甲只有可能在第1次和第3次取球,
记“甲第一次取到白球”的事件为A1,
“第3球取到白球”的事件为A3,
因为事件A1,A3两两互斥.
所以P=P(A1)+P(A3)=$\frac{C_3^1}{C_7^1}+\frac{A_4^2C_3^1}{A_7^3}=\frac{3}{7}+\frac{4×3×3}{7×6×5}=\frac{3}{5}$.…(8分)
(3)因为第四次轮到乙取球,“第四次乙取到白球”的事件为B,
“第四次乙取不到白球”的事件为C,
则P=$P(B)+P(C)=\frac{A_4^3C_3^1}{A_7^4}+\frac{A_4^4}{A_7^4}=\frac{3}{35}+\frac{1}{35}=\frac{4}{35}$…(12分).
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意对立事件概率计算公式、互斥事件概率加法公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.在△OAB中,已知OA=5,OB=4,点P是AB的中点,则$\overrightarrow{OP}•\overrightarrow{AB}$=( )
| A. | 10 | B. | -$\frac{9}{2}$ | C. | 20 | D. | -20 |
11.曲线$\left\{\begin{array}{l}x=5cosθ\\ y=4sinθ\end{array}$(θ为参数)的焦点到双曲线x2-$\frac{y^2}{2}$=1的渐近线的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{10}$ |
9.已知sinα=$\frac{{2\sqrt{2}}}{3}$,cos(α+β)=-$\frac{1}{3}$,且α,β∈(0,$\frac{π}{2}$),则sin(α-β)的值等于( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{3}$ | D. | $\frac{{10\sqrt{2}}}{27}$ |
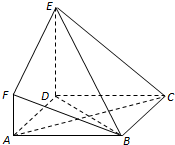 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3$\sqrt{6}$.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3$\sqrt{6}$.