题目内容
在正三棱锥P-ABC(顶点在底面的射影是底面正三角形的中心)中,AB=4,PA=8,过A作与PB,PC分别交于D和E的截面,则截面△ADE的周长的最小值是( )
分析:利用正三棱锥P-ABC的侧面展开图,即可将求△ADE的周长的最小值问题转化为求展开图中线段的长的问题,进而在三角形中利用解三角形的知识计算即可
解答:解:此正三棱锥的侧面展开图如图 :则△ADE的周长为AD+DE+EA′,由于两点之间线段最短,
:则△ADE的周长为AD+DE+EA′,由于两点之间线段最短,
∴当D、E处于如图位置时,截面△ADE的周长最小,即为AA′的长
设∠APB=α,过P作PO⊥AA′,则O为AA′中点,∠APO=
,
在等腰三角形PAB中,sin
=
=
,cos
=
∴cosα=1-2sin2
=
,sinα=2sin
•cos
=
∴sin
=sin(α+
)=sinαcos
+cosαsin
=
×
+
×
=
∴AA′=2AO=2AP×sin
=16×
=11
故选C
 :则△ADE的周长为AD+DE+EA′,由于两点之间线段最短,
:则△ADE的周长为AD+DE+EA′,由于两点之间线段最短,∴当D、E处于如图位置时,截面△ADE的周长最小,即为AA′的长
设∠APB=α,过P作PO⊥AA′,则O为AA′中点,∠APO=
| 3α |
| 2 |
在等腰三角形PAB中,sin
| α |
| 2 |
| 2 |
| 8 |
| 1 |
| 4 |
| α |
| 2 |
| ||
| 4 |
∴cosα=1-2sin2
| α |
| 2 |
| 7 |
| 8 |
| α |
| 2 |
| α |
| 2 |
| ||
| 8 |
∴sin
| 3α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| ||
| 8 |
| ||
| 4 |
| 7 |
| 8 |
| 1 |
| 4 |
| 11 |
| 16 |
∴AA′=2AO=2AP×sin
| 3α |
| 2 |
| 11 |
| 16 |
故选C
点评:本题考查了利用几何体的侧面展开图求截面周长最值的方法,利用三角变换公式解三角形的技巧,空间问题转化为平面问题的思想方法

练习册系列答案
相关题目
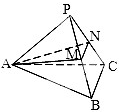 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|