题目内容
设
，函数
.
(1)当
时，求曲线
在点
处的切线方程；
(2)当
时，求函数
的最小值.
解:（1）当时，
，当
时，
令
，得
所以切点为（1，2），切线的斜率为1，
所以曲线在处的切线方程为：
.
（2）①当
时，
，
.
，
恒成立. 
在
上为增函数.
故当
时，
.
②当
时，
，
（）
(ⅰ)当
即
时，若
时，
，所以在区间
上为增函数.
故当时，
，且此时
.
(ⅱ)当
，即
时，若
时，
;
若
时,,
所以在区间
上为减函数，在
上为增函数，
故当
时，
，且此时
.
(ⅲ)当
；即
时，若时，,所以在区间[1,
]上为减函数，
故当时，.
综上所述，当时，在和上的最小值都是
,
所以在
上的最小值为
；
当时，在时的最小值为
，而，
所以在上的最小值为.
当时，在时最小值为，在时的最小值为
，
而, 所以在上的最小值为.
所以函数的最小值为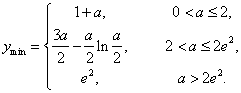
练习册系列答案
文敬图书课时先锋系列答案
相关题目
叫做幂函数。幂函数
时，在
上是增函数；当
时，在
上是减函数。 设幂函数
，证明：当
时，有
；
，对任意的
，证明
；
，函数
时，试确定函数
的单调区间；
，且
都有
，求
的取值范围.
，函数
.
，求函数
的单调区间；
的取值范围。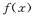
在[-1,1]上是增函数，且
，若函数
1对所有
都成立，则当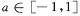
时t的取值范围是____ 
，函数
的奇偶性；
的单调性，并加以证明。