题目内容
在△ABC中，设命题p：| a |
| sinB |
| b |
| sinC |
| c |
| sinA |
分析：利用命题p：
=
=
；以及正弦定理，求出sinA=sinB=sinC，推出△ABC是等边三角形，反之可逆推．
| a |
| sinB |
| b |
| sinC |
| c |
| sinA |
解答：解：命题p：
=
=
．由正弦定理
=
=
，得sinA=sinB=sinC，
∴A=B=C?a=b=C、反之，亦成立．
故答案为：充分必要
| a |
| sinB |
| b |
| sinC |
| c |
| sinA |
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴A=B=C?a=b=C、反之，亦成立．
故答案为：充分必要
点评：本题是基础题，考查三角函数与正弦定理的应用，考查计算能力逻辑推理能力，常考题型．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，设命题p：
=
=
，命题q：△ABC是等边三角形，那么命题p是命题q的（ ）
| a |
| sinB |
| b |
| sinC |
| c |
| sinA |
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、即不充分也不必要条件 |
命题q:△ABC是等边三角形，那么命题p是命题q的（ ） 
，命题q：△ABC是等边三角形，那么命题p是命题q的（ ）
=
=
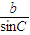；命题q：△ABC是等边三角形．那么命题p是命题q的 条件．