题目内容
长为2的线段AB的两个端点在抛物线y2=x上滑动,则线段AB中点M到y轴距离的最小值是
.
| 3 |
| 4 |
| 3 |
| 4 |
分析:设A、B、M抛物线的准线上的射影分别为C、D、N,连结AC、BD、MN.根据梯形中位线定理证出|MN|=
(|AC|+|BD|),利用抛物线的定义得|AC|+|BD|=|AF|+|BF|,由此结合平面几何的知识证出|MN|≥
|AB|=1,即可求出AB中点M到y轴距离的最小值.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设抛物线的准线为l,A、B、M在l上的射影分别为C、D、N,连结AC、BD、MN.
由梯形的中位线定理,可得|MN|=
(|AC|+|BD|)
连结AF、BF,根据抛物线的定义得|AF|=|AC|,|BF|=|BD|
根据平面几何知识,可得|AF|+|BF|≥|AB|,
当且仅当点F在AB上时取等号
∴|AC|+|BD|≥|AB|=2,
可得|MN|=
(|AC|+|BD|)≥
|AB|=1
设M的横坐标为a,则|MN|=a+
≥1,得a≥
.
因此,当且仅当线段AB为抛物线经过焦点的弦时,
AB中点M到y轴距离的最小值为
故答案为:

由梯形的中位线定理,可得|MN|=
| 1 |
| 2 |
连结AF、BF,根据抛物线的定义得|AF|=|AC|,|BF|=|BD|
根据平面几何知识,可得|AF|+|BF|≥|AB|,
当且仅当点F在AB上时取等号
∴|AC|+|BD|≥|AB|=2,
可得|MN|=
| 1 |
| 2 |
| 1 |
| 2 |
设M的横坐标为a,则|MN|=a+
| 1 |
| 4 |
| 3 |
| 4 |
因此,当且仅当线段AB为抛物线经过焦点的弦时,
AB中点M到y轴距离的最小值为
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题给出抛物线长度为2的弦,当弦在抛物线上滑动时求它的中点到y轴的最小距离.着重考查了抛物线的定义、标准方程和简单几何性质等知识,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
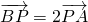 .
. 的直线l'交曲线C于另一R点.求证:直线NR与直线OQ的交点为定点(O为坐标原点),并求出该定点.
的直线l'交曲线C于另一R点.求证:直线NR与直线OQ的交点为定点(O为坐标原点),并求出该定点. ,
, 的直线l′交曲线C于另一点R。求证:直线NR与直线OQ的交点为定点(O为坐标原点),并求出该定点。
的直线l′交曲线C于另一点R。求证:直线NR与直线OQ的交点为定点(O为坐标原点),并求出该定点。 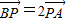 .
.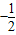 的直线l'交曲线C于另一R点.求证:直线NR与直线OQ的交点为定点(O为坐标原点),并求出该定点.
的直线l'交曲线C于另一R点.求证:直线NR与直线OQ的交点为定点(O为坐标原点),并求出该定点.