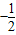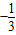题目内容
已知实数a，b满足等式(
)a=(
)b，则下列五个关系式：①0＜b＜a②a＜b＜0③0＜a＜b④b＜a＜0⑤a=b其中可能成立的关系为
| 1 |
| 2 |
| 1 |
| 3 |
①、②、⑤
①、②、⑤
（用编号作答）．分析：令(
)a=(
)b=t则根据指数式与对数式的互化可得a=
，b=
然后在统一直角坐标系中作出y=
，y=
的图象则根据图象即可比较出a，b的大小．
| 1 |
| 2 |
| 1 |
| 3 |
| log | t
|
| log | t
|
| log | t
|
| log | t
|
解答：
解：令(
)a=(
)b=t
则a=
，b=
在同一直角坐标系中作出则y=
，y=
的图象（如右图）：
则根据图象可得当0＜t＜1时0＜b＜a
当t=1时a=b
当t＞l时a＜b＜0
故答案为①②⑤
解：令(| 1 |
| 2 |
| 1 |
| 3 |
则a=
| log | t
|
| log | t
|
在同一直角坐标系中作出则y=
| log | t
|
| log | t
|
则根据图象可得当0＜t＜1时0＜b＜a
当t=1时a=b
当t＞l时a＜b＜0
故答案为①②⑤
点评：本题主要考察了对数函数的性质，属中等题目．解题的关键是利用指数式与对数式的互化将a，b的大小比较转化为比较对数值
，
的大小！
| log | t
|
| log | t
|
练习册系列答案
全能测控期末小状元系列答案
智趣暑假温故知新系列答案
相关题目
已知实数a、b满足条件：ab＜0，且1是a2与b2的等比中项，又是
，
的等差中项，则
的值是（ ）
| 1 |
| a |
| 1 |
| b |
| a+b |
| a2+b2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
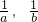的等差中项，则
的值是
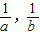的等差中项，则
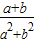的值是（ ）
