题目内容
如图,建立直角坐标系,已知正方体ABCD—A′B′C′D′的棱长为a,M是棱AA′的中点,点O是对角线BD′的中点.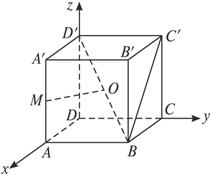
(1)证明:OM是异面直线AA′和BD′的公垂线;
(2)求异面直线MO和BC′所成的角的大小.
(1)证明:M(a,0,![]() ),O(
),O(![]() ,
,![]() ,
,![]() ),A(a,0,0),A′(a,0,a),B(a,a,0),D′(0,0,a),C′(0,a,a).
),A(a,0,0),A′(a,0,a),B(a,a,0),D′(0,0,a),C′(0,a,a).
∴![]() =(
=(![]() ,-
,-![]() ,0),
,0), ![]() =(0,0,a),
=(0,0,a),![]() =(-a,-a,a).
=(-a,-a,a).
∴![]() ·
·![]() =0,
=0, ![]() ·
·![]() =-
=-![]() +
+![]() =0.
=0.
∴![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() .
.
∴OM是异面直线AA′和BD′的公垂线.
(2)解:由(1)知![]() =(-a,0,a),
=(-a,0,a),
∴cos〈![]() ,
,![]() 〉=
〉= =
=
=![]() =-
=-![]() .
.
∴〈![]() ,
,![]() 〉=120°.
〉=120°.
∴异面直线![]() 和
和![]() 所成的角为60°.
所成的角为60°.

练习册系列答案
相关题目
 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,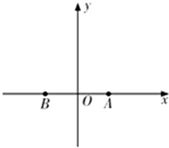 为了加快县域经济的发展,某县选择两乡镇作为龙头带动周边乡镇的发展,决定在这两个镇的周边修建环形高速公路,假设一个单位距离为10km,两镇的中心A、B相距8个单位距离,环形高速公路所在的曲线为E,且E上的点到A、B的距离之和为10个单位距离,在曲线E上建一个加油站M与一个收费站N,使M、N、B三点在一条直线上,并且AM+AN=12个单位距离.
为了加快县域经济的发展,某县选择两乡镇作为龙头带动周边乡镇的发展,决定在这两个镇的周边修建环形高速公路,假设一个单位距离为10km,两镇的中心A、B相距8个单位距离,环形高速公路所在的曲线为E,且E上的点到A、B的距离之和为10个单位距离,在曲线E上建一个加油站M与一个收费站N,使M、N、B三点在一条直线上,并且AM+AN=12个单位距离.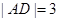 ,
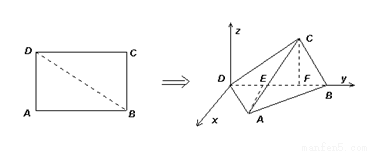
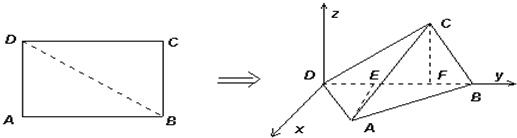
,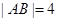 .将矩形ABCD沿对角线BD折起,使得面BCD⊥面ABD.现以D为原点,DB作为y轴的正方向,建立如图空间直角坐标系,此时点A恰好在xDy坐标平面内.试求A,C两点的坐标.
.将矩形ABCD沿对角线BD折起,使得面BCD⊥面ABD.现以D为原点,DB作为y轴的正方向,建立如图空间直角坐标系,此时点A恰好在xDy坐标平面内.试求A,C两点的坐标.