题目内容
下面四个命题:
①已知函数f(x)=
且f(a)+f(4)=4,那么a=-4;
②要得到函数y=sin(2x+
)的图象,只要将y=sin2x的图象向左平移
单位;
③若定义在(-∞,+∞)上的函数f(x)满足f(x+1)=-f(x),则f(x)是周期函数;
④已知奇函数f(x)在(0,+∞)为增函数,且f(-1)=0,则不等式f(x)<0的解集{x|x<-1}.
其中正确的是 .
①已知函数f(x)=
|
②要得到函数y=sin(2x+
| π |
| 3 |
| π |
| 3 |
③若定义在(-∞,+∞)上的函数f(x)满足f(x+1)=-f(x),则f(x)是周期函数;
④已知奇函数f(x)在(0,+∞)为增函数,且f(-1)=0,则不等式f(x)<0的解集{x|x<-1}.
其中正确的是
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:由分段函数函数值的求法结合f(a)+f(4)=4分类求解a的值判断①;
把函数y=sin(2x+
)变形为sin[2(x+
)],看自变量的变化判断②;
由已知条件求出函数周期判断③;
结合函数的单调性与奇偶性求得不等式f(x)<0的解集判断④.
把函数y=sin(2x+
| π |
| 3 |
| π |
| 6 |
由已知条件求出函数周期判断③;
结合函数的单调性与奇偶性求得不等式f(x)<0的解集判断④.
解答:
解:对于①,∵f(x)=
,
∴f(4)=2,
又f(a)+f(4)=4,
∴f(a)=2.
若a≥0,则f(a)=
=2,a=4.
若a<0,则f(a)=
=2,a=-4.∴命题①错误;
对于②,∵y=sin(2x+
)=sin[2(x+
)],
∴要得到函数y=sin(2x+
)的图象,只要将y=sin2x的图象向左平移
单位.∴命题②错误;
对于③,若定义在(-∞,+∞)上的函数f(x)满足f(x+1)=-f(x),
则f(x+2)=f(x+1+1)=-f(x+1)=-[-f(x)]=f(x).
∴f(x)是周期为2的周期函数.命题③正确;
对于④,奇函数f(x)在(0,+∞)为增函数,则f(x)在(-∞,0)上为增函数,
又f(-1)=0,
∴f(1)=0,
则不等式f(x)<0的解集{x|x<-1或0<x<1}.∴命题④错误.
∴正确的命题是③.
故答案为:③.
|
∴f(4)=2,
又f(a)+f(4)=4,
∴f(a)=2.
若a≥0,则f(a)=
| a |
若a<0,则f(a)=
| -a |
对于②,∵y=sin(2x+
| π |
| 3 |
| π |
| 6 |
∴要得到函数y=sin(2x+
| π |
| 3 |
| π |
| 6 |
对于③,若定义在(-∞,+∞)上的函数f(x)满足f(x+1)=-f(x),
则f(x+2)=f(x+1+1)=-f(x+1)=-[-f(x)]=f(x).
∴f(x)是周期为2的周期函数.命题③正确;
对于④,奇函数f(x)在(0,+∞)为增函数,则f(x)在(-∞,0)上为增函数,
又f(-1)=0,
∴f(1)=0,
则不等式f(x)<0的解集{x|x<-1或0<x<1}.∴命题④错误.
∴正确的命题是③.
故答案为:③.
点评:本题考查了命题的真假判断与应用,考查了函数的性质,解答此题的关键在于对函数性质的理解与应用,是中档题.

练习册系列答案
相关题目
从一堆苹果中任取了20个,并得到它们的质量(单位:克)数据分布表如下:
则这堆苹果中,质量不小于120克的苹果数约占苹果总数的( )
| 分组 | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 1 | 2 | 3 | 10 | 3 | 1 |
| A、30% | B、70% |
| C、60% | D、50% |
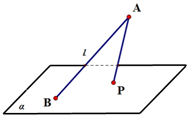 如图,点A是平面α外一定点,过A作平面α的斜线l,斜线l与平面α所成角为50°.若点P在平面α内运动,并使直线AP与l所成角为35°,则动点P的轨迹是( )
如图,点A是平面α外一定点,过A作平面α的斜线l,斜线l与平面α所成角为50°.若点P在平面α内运动,并使直线AP与l所成角为35°,则动点P的轨迹是( )| A、圆 | B、椭圆 |
| C、抛物线 | D、双曲线的一支 |
双曲线
-
=1(a>0,b>0)的一个焦点F到它的一条渐近线距离x满足a≤x≤3a,则该双曲线的离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(
| ||||
B、(1,
| ||||
C、[2,
| ||||
D、[
|