Question

11．在直线l：x+y-3=0上求一点P，使P到点A（2，0），B（-2，-2）的距离之和最小．

Answer 1

分析 求出A关于直线l：x+y-3=0的对称点为C，则P为直线BC与直线l的交点时，满足条件，进而得到答案．

解答 解：如下图所示：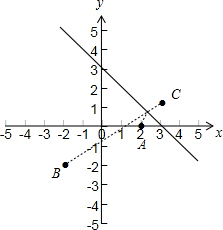

点A（2，0），关于直线l：x+y-3=0的对称点为C（3，1）点，
由BC的方程为：$\frac{x+2}{5}=\frac{y+2}{3}$，即3x-5y-4=0，
可得直线BC与直线l的交点坐标为：（$\frac{19}{8}$，$\frac{5}{8}$），
即P点坐标为：（$\frac{19}{8}$，$\frac{5}{8}$）时，P到点A（2，0），B（-2，-2）的距离之和最小．

点评 本题考查的知识点是两点间距离公式的应用，难度不大，属于中档题．