题目内容
圆M的圆心在直线y=-2x上,且与直线x+y=1相切于点A(2,-1),
(1)试求圆M的方程;
(2)过原点的直线l与圆M相交于B,C两点,且|BC|=2,求直线l的方程.
(1)试求圆M的方程;
(2)过原点的直线l与圆M相交于B,C两点,且|BC|=2,求直线l的方程.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)由题意知:过A(2,-1)且与直线x+y=1垂直的直线方程为:y=x-3,确定圆心与半径,即可求圆M的方程;
(2)分两种情况考虑:①当直线l的斜率不存在时,显然经检验x=0满足题意;②当直线l的斜率存在时,设直线l的方程为y=kx,由弦长的一半及圆的半径,利用勾股定理列出关于k的方程,求出方程的解得到k的值,确定出直线l的方程.
(2)分两种情况考虑:①当直线l的斜率不存在时,显然经检验x=0满足题意;②当直线l的斜率存在时,设直线l的方程为y=kx,由弦长的一半及圆的半径,利用勾股定理列出关于k的方程,求出方程的解得到k的值,确定出直线l的方程.
解答:
解:(1)由题意知:过A(2,-1)且与直线x+y=1垂直的直线方程为:y=x-3
∵圆心在直线:y=-2x上,∴由
⇒
,
即M(1,-2),且半径r=|AO1|=
=
,
∴所求圆的方程为:(x-1)2+(y+2)2=2(得圆心给2分)(6分)
(2)①当斜率不存在时,直线方程是x=0,圆心到直线的距离为1,|BC|=2所以x=0满足题意…(9分)
②当斜率存在时,设直线方程y=kx,
由BC=2
=2得k=-
,
所以直线方程为y=-
x所以所求直线方程为x=0,y=-
x…(14分)
∵圆心在直线:y=-2x上,∴由
|
|
即M(1,-2),且半径r=|AO1|=
| (2-1)2+(-1+2)2 |
| 2 |
∴所求圆的方程为:(x-1)2+(y+2)2=2(得圆心给2分)(6分)
(2)①当斜率不存在时,直线方程是x=0,圆心到直线的距离为1,|BC|=2所以x=0满足题意…(9分)
②当斜率存在时,设直线方程y=kx,
由BC=2
2-(
|
| 3 |
| 4 |
所以直线方程为y=-
| 3 |
| 4 |
| 3 |
| 4 |
点评:此题考查了圆的切线方程,涉及的知识有:圆的标准方程,点到直线的距离公式,垂径定理,以及勾股定理,利用了分类讨论的思想,要求学生考虑问题要全面,做到不重不漏.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
若数列{an}的通项公式为an=
,其前n项和为
,则n为( )
| 1 |
| (n+1)(n+2) |
| 7 |
| 18 |
| A、5 | B、6 | C、7 | D、8 |
如果(3x+2)5=a0x5+a1x4+a2x3+a3x2+a4x+a5,那么a0-a1+a2-a3+a4的值等于( )
| A、33 | ||
| B、-31 | ||
C、
| ||
D、
|
直线l:kx+(1-k)y-3=0经过的定点是( )
| A、(0,1) |
| B、(3,3) |
| C、(1,-3) |
| D、(1,1) |
已知圆C过定点A(0,4),且圆心C在抛物线x2=8y上运动,则x轴被圆C所截得的弦长为( )
| A、8 | B、6 |
| C、4 | D、与圆心C的位置有关 |
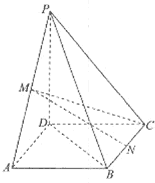 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,M、N分别为PA、BC的中点,且PD=AD=1,
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,M、N分别为PA、BC的中点,且PD=AD=1,