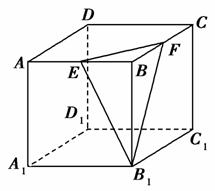
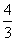题目内容
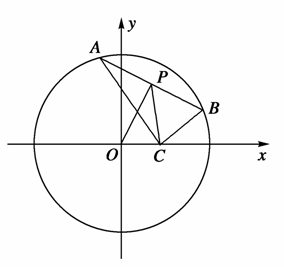
已知点C(1,0),点A、B是⊙O:x2+y2=9上任意两个不同的点,且满足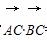 =0,设P为弦AB的中点.
=0,设P为弦AB的中点.
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线x=-1的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
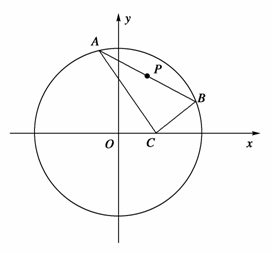
(1)法一:连接CP,由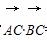 =0知,AC⊥BC,∴|CP|=|AP|=|BP|=
=0知,AC⊥BC,∴|CP|=|AP|=|BP|=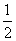 |AB|,
|AB|,
由垂径定理知|OP|2+|AP|2=|OA|2,即|OP|2+|CP|2=9,
设点P(x,y),有(x2+y2)+[(x-1)2+y2]=9,
化简得,x2-x+y2=4.
法二:设A(x1,y1),B(x2,y2),P(x,y),
根据题意知,x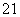 +y
+y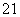 =9,x
=9,x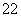 +y
+y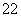 =9,2x=x1+x2,2y=y1+y2,
=9,2x=x1+x2,2y=y1+y2,
∴4x2=x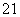 +2x1x2+x
+2x1x2+x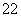 ,4y2=y
,4y2=y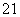 +2y1y2+y
+2y1y2+y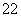 ,
,
故4x2+4y2=(x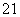 +y
+y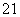 )+(2x1x2+2y1y2)+(x
)+(2x1x2+2y1y2)+(x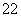 +y
+y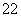 )=18+2(x1x2+y1y2),①
)=18+2(x1x2+y1y2),①
又∵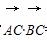 =0,∴(1-x1,-y1)·(1-x2,-y2)=0,
=0,∴(1-x1,-y1)·(1-x2,-y2)=0,
∴(1-x1)×(1-x2)+y1y2=0,故x1x2+y1y2=(x1+x2)-1=2x-1,
代入①式得,4x2+4y2=18+2(2x-1),
化简得,x2-x+y2=4.
(2)根据抛物线的定义,到直线x=-1的距离等于到点C(1,0)的距离的点都在抛物线y2=2px上,其中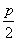 =1,∴p=2,故抛物线方程为y2=4x,
=1,∴p=2,故抛物线方程为y2=4x,
由方程组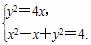 得,x2+3x-4=0,
得,x2+3x-4=0,
解得x1=1,x2=-4,
由于x≥0,故取x=1,此时y=±2,
故满足条件的点存在,其坐标为(1,-2)和(1,2).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
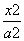 +
+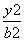 =1(a>0,b>0)的左焦点,若椭圆上存在点P,使得直线PF与圆x2+y2=b2相切,当直线PF的倾斜角为
=1(a>0,b>0)的左焦点,若椭圆上存在点P,使得直线PF与圆x2+y2=b2相切,当直线PF的倾斜角为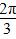 时,此椭圆的离心率是________.
时,此椭圆的离心率是________.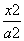 -
-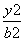 =1与直线y=2x有交点,则双曲线离心率的取值范围为( )
=1与直线y=2x有交点,则双曲线离心率的取值范围为( )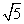 ) B.(1,
) B.(1, x2上的动点,点P在x轴上的射影为M,点A的坐标是(2,0),则|PA|+|PM|的最小值是________.
x2上的动点,点P在x轴上的射影为M,点A的坐标是(2,0),则|PA|+|PM|的最小值是________. =1的两条渐近线和抛物线y2=-8x的准线所围成的三角形(含边界与内部).若点(x,y)∈D,则x+y的最小值为( )
=1的两条渐近线和抛物线y2=-8x的准线所围成的三角形(含边界与内部).若点(x,y)∈D,则x+y的最小值为( ) -1)=0表示的曲线是( )
-1)=0表示的曲线是( ) x和y=-
x和y=- ,P是AB的中点,则动点P的轨迹C的方程为________.
,P是AB的中点,则动点P的轨迹C的方程为________.
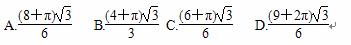
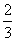 B.
B.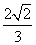
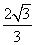 D.
D.