Question

【题目】在如图所示的多面体中，已知， ， 是正三角形， ， ， 是的中点.

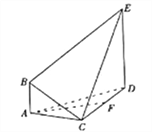
（1）求证： 平面；

（2）求证：平面平面；

（3）求到平面的距离.

Answer 1

【答案】(1)见解析；（2）见解析；（3）D到平面BCE的距离为.

【解析】【试题分析】（1）取的中点，连接，利用三角形的中位线，可证得，即四边形为平行四边形，所以，所以平面.（2）通过计算证明，而，故平面，故，也即，结合可知平面，也即平面，故平面平面.（3）连接，由（2）的结论，易知就是所求的距离.

【试题解析】

（Ⅰ）取的中点，连接，因为的中点，

所以，又AB ,

所以，四边形为平行四边形，

所以MB//AF,

因为平面， 平面，

所以平面

（Ⅱ）因为是正三角形，所以,

在中， ，

所以，故，

∴DE⊥AC，又DE⊥AD,AC∩AD=A

∴DE⊥平面ACD

∴DE⊥AF,又AF⊥CD，由（Ⅰ）得BM∥AF

∴DE⊥BM, BM⊥CD，DE∩CD=D

∴BM⊥平面CDE，BM平面BCE

∴平面BCE⊥平面CDE

（Ⅲ）连接DM，由于DE=DC

∴DM⊥CE

由（Ⅱ）知，平面BCE⊥平面CDE，

∴DM⊥平面BCE

所以DM为D到平面BCE的距离，DM=

所以D到平面BCE的距离为