题目内容
18.已知命题p:A={x|a-1<x<a+1,x∈R},命题q:B={x|x2-4x+3≥0}.若非q是p的必要条件,求实数a的取值范围.分析 根据不等式的解法求出命题p,q的等价条件,然后利用必要条件的定义,即可求a的取值范围.
解答 解:∵命题p:A={x|a-1<x<a+1,x∈R},
命题q:B={x|x2-4x+3≥0}.
非q:{x|1<x<3,x∈R},
∵非q是p的必要条件
则$\left\{\begin{array}{l}{a-1≥1}\\{a+1≤3}\end{array}\right.$
可得a=2
∴实数a的取值范围:a=2.
点评 本题主要考查充分条件和必要条件的应用,利用不等式的性质求出命题p,q的等价条件是解决本题的关键

练习册系列答案
相关题目
6.定义在R上的函数f(x)既是奇函数又是周期函数,若f(x)的最小正周期是π,且当$x∈[0,\frac{π}{2})$时,f(x)=sinx,则$f(\frac{8}{3}π)$的值为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |
13.函数y=x2(x-3)的单调递减区间是( )
| A. | (-∞,0) | B. | (2,+∞) | C. | (0,2) | D. | (-2,2) |
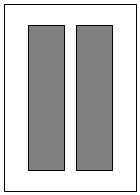 如图,要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,设广告牌的高为xcm,宽为ycm
如图,要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,设广告牌的高为xcm,宽为ycm