题目内容
等差数列{an}中，若a3+a4+a5+a6+a7=50，则a1+a9等于（ ）
| A、5 | B、15 | C、30 | D、20 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：根据题意中等差数列的连续五项之和的值，利用等差中项做出第五项的值，要求的两项的和等于第五项的二倍，代入数值得到结果．
解答：
解：∵a3+a4+a5+a6+a7=50，
∴5a5=50
∴a5=10
∴a1+a9=2a5=20，
故选D．
∴5a5=50
∴a5=10
∴a1+a9=2a5=20，
故选D．
点评：本题考查等差中项的性质，本题解题的关键是写出等差中项的值，本题是一个基础题．
练习册系列答案
相关题目
三角形ABC周长等于20，面积等于10
，∠A=60°，则∠A所对边长a为（ ）
| 3 |
| A、5 | B、7 | C、6 | D、8 |
表示实心圆，
表示空心圆）：
已知圆心为点C（4，7），并且在直线3x-4y+1=0上截得的弦长为8的圆的方程为（ ）
| A、（x-4）2+（y-7）2=5 |
| B、（x-4）2+（y-7）2=25 |
| C、（x-7）2+（y-4）2=5 |
| D、（x-7）2+（y-4）2=25 |
定义在（0，+∞）上函数f（x）满足对任意x，y∈（0，+∞），都有xyf（xy）=xf（x）+yf（y），记数列an=f（2n），有以下命题：
①f（1）=0；
②a1=a2；
③令函数g（x）=xf（x），则g（x）+g（
）=0；
④令数列bn=2n•an，则数列{bn}为等比数列．
其中正确命题的为（ ）
①f（1）=0；
②a1=a2；
③令函数g（x）=xf（x），则g（x）+g（
| 1 |
| x |
④令数列bn=2n•an，则数列{bn}为等比数列．
其中正确命题的为（ ）
| A、①②③ | B、①② |
| C、②③ | D、①②③④ |
某市出租车起步价为5元（起步价内行驶里程为3km），以后每1km价为1.8元 （不足1km按1km计价），则乘坐出租车的费用y（元）与行驶的里程x（km）之间的函数图象大致为下列图中的（ ）
A、 |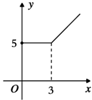
B、 |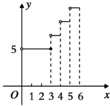
C、 |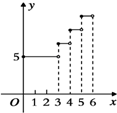
D、 |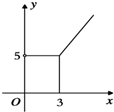
命题“若α=
，则sinα=1”的逆否命题是（ ）
| π |
| 2 |
A、若α≠
| ||
B、若α=
| ||
C、若sinα≠1，则α≠
| ||
D、若sinα≠1，则α=
|
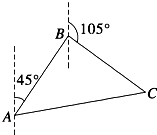如图所示，我艇在A处发现一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃窜，我艇立即以14海里/小时的速度追击，求我艇追上走私船所需要的最短时间．