题目内容
设a是实数，且
+i3是实数，则a等于（ ）
| a |
| 1-i |
| A、-1 | B、0 | C、1 | D、2 |
考点：复数代数形式的混合运算,复数的基本概念
专题：数系的扩充和复数
分析：利用复数的幂运算，以及复数分母实数化，通过复数是实数虚部为0 求出a即可．
解答：
解：
+i3=
-i=
-i=
+(
-1)i．
因为复数是实数，所以
-1=0，∴a=2．
故选：D．
| a |
| 1-i |
| a+ai |
| (1-i)(1+i) |
| a+ai |
| 2 |
| a |
| 2 |
| a |
| 2 |
因为复数是实数，所以
| a |
| 2 |
故选：D．
点评：本题考查复数代数形式的混合运算，复数的基本概念，基础题．
练习册系列答案
相关题目
实数x，y满足
，则x+y的取值范围是（ ）
|
| A、[0，2] | ||
B、[
| ||
C、[0，
| ||
| D、（-∞，2] |
执行如图程序框图，则输出的n值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
一个几何体的三视图如图所示，则这个几何体的体积为（ ）
A、
| ||
B、
| ||
| C、8 | ||
D、
|
在非钝角△ABC中，C=
，则cos2A+cos2B的最小值为（ ）
| π |
| 3 |
A、1-
| ||||
B、
| ||||
C、1-
| ||||
D、1+
|
圆O的弦AB，CD相交于点P，已知P是AB的中点，AB=12，PC=4，那么PD=（ ）
| A、16 | B、9 | C、8 | D、4 |
已知a，b∈R，下列四个条件中，使a＜b成立的必要而不充分的条件是（ ）
| A、|a|＜|b| |
| B、2a＜2b |
| C、a＜b-1 |
| D、a＜b+1 |
若P的Q的北偏东44°50′，则Q在P的（ ）
| A、东偏北45°10′ |
| B、东偏北45°50′ |
| C、南偏西44°50′ |
| D、西偏南45°50′ |
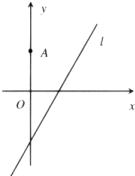如图，在平面直角坐标系xOy中，点A（0，3），直线l：y=2x-4，设圆C的半径为1，圆心在直线l上．