题目内容
椭圆C: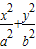 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为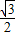 ,且椭圆上动点P到左焦点距离的最大值为
,且椭圆上动点P到左焦点距离的最大值为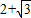 .
.(I)求椭圆C的方程;
(II)斜率不为0的直线l与椭圆C交于M、N两点,定点A(0,1),若|AM|=|AN|,求直线l的斜率k的取值范围.
【答案】分析:(I)利用椭圆C: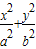 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为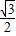 ,且椭圆上动点P到左焦点距离的最大值为
,且椭圆上动点P到左焦点距离的最大值为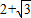 ,建立方程组,求得几何量,即可求椭圆C的方程;
,建立方程组,求得几何量,即可求椭圆C的方程;
(II)利用点差法,结合|AM|=|AN|,可得AE⊥MN,从而可得E的坐标,利用E在椭圆内部,建立不等式,即可求直线l的斜率k的取值范围.
解答:解:(I)∵椭圆C: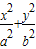 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为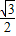 ,且椭圆上动点P到左焦点距离的最大值为
,且椭圆上动点P到左焦点距离的最大值为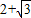
∴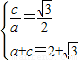 ,∴
,∴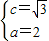 ,∴b=1
,∴b=1
∴椭圆C的方程为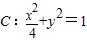 …(4分)
…(4分)
(II)设M(x1,y1),N(x2,y2),其中点E(x,y),则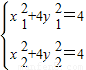
两方程相减可得(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0
∴x+4yk=0①
又AE⊥MN,故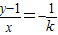 ,即x+ky=k②
,即x+ky=k②
由①②知,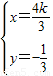 ,即
,即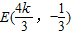 ,…(8分)
,…(8分)
∵E在椭圆内部,∴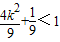
∴k2<2…(10分)
又k≠0,故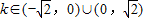 …(12分)
…(12分)
点评:本题考查椭圆的性质与标准方程,考查点差法的运用,考查学生的计算能力,正确运用点差法是关键.
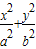 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为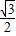 ,且椭圆上动点P到左焦点距离的最大值为
,且椭圆上动点P到左焦点距离的最大值为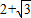 ,建立方程组,求得几何量,即可求椭圆C的方程;
,建立方程组,求得几何量,即可求椭圆C的方程;(II)利用点差法,结合|AM|=|AN|,可得AE⊥MN,从而可得E的坐标,利用E在椭圆内部,建立不等式,即可求直线l的斜率k的取值范围.
解答:解:(I)∵椭圆C:
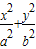 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为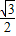 ,且椭圆上动点P到左焦点距离的最大值为
,且椭圆上动点P到左焦点距离的最大值为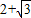
∴
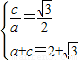 ,∴
,∴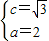 ,∴b=1
,∴b=1∴椭圆C的方程为
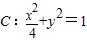 …(4分)
…(4分)(II)设M(x1,y1),N(x2,y2),其中点E(x,y),则
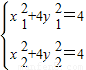
两方程相减可得(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0
∴x+4yk=0①
又AE⊥MN,故
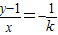 ,即x+ky=k②
,即x+ky=k②由①②知,
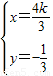 ,即
,即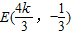 ,…(8分)
,…(8分)∵E在椭圆内部,∴
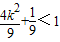
∴k2<2…(10分)
又k≠0,故
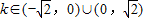 …(12分)
…(12分)点评:本题考查椭圆的性质与标准方程,考查点差法的运用,考查学生的计算能力,正确运用点差法是关键.

练习册系列答案
相关题目
 =1(a>b>0)的离心率
=1(a>b>0)的离心率 ,直线
,直线 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切. ,-l).
,-l). +
+ =1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e.
=1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e. ,且恰好经过椭圆的右顶点,求e的大小;
,且恰好经过椭圆的右顶点,求e的大小; y+3=0相切,求椭圆方程.
y+3=0相切,求椭圆方程.
 +
+ =1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e.
=1(a>b>0),直线l为圆O:x2+y2=b2的一条切线,记椭圆C的离心率为e. ,且恰好经过椭圆的右顶点,求e的大小;
,且恰好经过椭圆的右顶点,求e的大小; y+3=0相切,求椭圆方程.
y+3=0相切,求椭圆方程.
 =1(a>b>0)的左、右两个焦 点。(1)若椭圆C上的点A(1,
=1(a>b>0)的左、右两个焦 点。(1)若椭圆C上的点A(1, )到F1、F2两点的 距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的 距离之和等于4,写出椭圆C的方程和焦点坐标; =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为
 :
: 与
与 轴交于点T,P为
轴交于点T,P为 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.