题目内容
5.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),若b3=11,{bn}的前9项和为153,则数列{bn}的通项公式为bn=3n+2.分析 数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),即2bn+1=bn+2+bn,可得:此数列是等差数列,设公差为d.根据b3=11,{bn}的前9项和为153,可得b1+2d=11,9b1+$\frac{9×8}{2}$d=153,联立解出即可得出.
解答 解:∵数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),即2bn+1=bn+2+bn,
∴此数列是等差数列,设公差为d.
∵b3=11,{bn}的前9项和为153,
∴b1+2d=11,9b1+$\frac{9×8}{2}$d=153,
联立解得b1=5,d=3.
则数列{bn}的通项公式为bn=5+3(n-1)=3n+2.
故答案为:3n+2.
点评 本题考查了等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.设O,A,B,M为平面上四点,$\overrightarrow{OM}$=$\frac{1}{3}$$\overrightarrow{OA}$$+\frac{2}{3}$$\overrightarrow{OB}$,则( )
| A. | 点B在线段AM上 | B. | 点M为线段BA的靠近B的三等分点 | ||
| C. | 点M为线段BA的中点 | D. | O,A,B,M四点共线 |
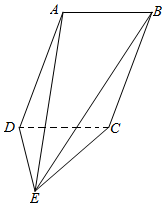 如图,平行四边形ABCD⊥平面CDE,AD=DC=DE=4,∠ADC=60°,AD⊥DE
如图,平行四边形ABCD⊥平面CDE,AD=DC=DE=4,∠ADC=60°,AD⊥DE