题目内容
设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点.若|AF|=3|BF|,则l的方程为( )
(A)y=x-1或y=-x+1
(B)y=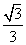 (x-1)或y=-
(x-1)或y=-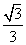 (x-1)
(x-1)
(C)y=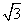 (x-1)或y=-
(x-1)或y=-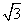 (x-1)
(x-1)
(D)y= (x-1)或y=-
(x-1)或y=- (x-1)
(x-1)
C
【解析】设A(x1,y1),B(x2,y2),
又F(1,0),
则 =(1-x1,-y1),
=(1-x1,-y1), =(x2-1,y2),
=(x2-1,y2),
由题意知 =3
=3 ,
,
因此
即
又由A、B均在抛物线上知
解得
直线l的斜率为 =±
=±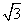 ,
,
因此直线l的方程为y=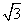 (x-1)或y=-
(x-1)或y=-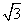 (x-1).
(x-1).
故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 对应的点的坐标在
对应的点的坐标在 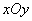 中,曲线
中,曲线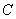 的参数方程为
的参数方程为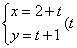 为参数),以该直角坐标系的原点为极点,
为参数),以该直角坐标系的原点为极点,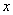 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线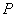 的方程为
的方程为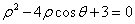 .
.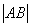 .
. 没有零点,则a的取值范围是________.
没有零点,则a的取值范围是________. 的一个极值点在区间
的一个极值点在区间 内,则实数
内,则实数 的取值范围是()
的取值范围是() B.
B. C.
C. D.
D.
 在定义域(—2,4)内可导,其图象
在定义域(—2,4)内可导,其图象 的导函数为
的导函数为 ,则不等
,则不等
 的解集为 。
的解集为 。 R
R ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 .
. 的解析式;
的解析式; 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 在点
在点 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( ) B.
B. C.
C. D.
D.