Question

设函数f（x）=log₄x-（

1

4

）^x，g（x）=log

1

4

x-(

1

4

)x的零点分别为x₁，x₂，则（　　）

A．x₁x₂=1

B．0＜x₁x₂＜1

C．1＜x₁x₂＜2

D．x₁x₂＞2

Answer 1

分析：由题意可得x₁是函数y=log₄x的图象和y=（

1

4

）^x的图象的交点的横坐标，x₂是y=log

1

4

x的图象和函数y
=（

1

4

）^x的图象的交点的横坐标，根据log

1

4

x₂＞log₄x₁，求得0＜x₁•x₂＜1，从而得出结论．

解答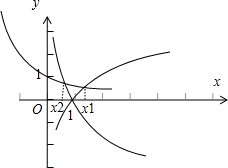：解：由题意可得x₁是函数y=log₄x的图象和y=（

1

4

）^x的图象的交点的横坐标，
x₂是y=log

1

4

x的图象和函数y=y=（

1

4

）^x的图象的交点的横坐标，且x₁，x₂都是正实数，如图所示：
故有log

1

4

x₂＞log₄x₁，故 log₄x₁-log

1

4

x₂＜0，∴log₄x₁+log₄x₂＜0，
∴log₄（x₁•x₂）＜0，∴0＜x₁•x₂＜1，
故选B．

点评：本题主要考查对数函数、指数函数的图象和性质应用，体现了数形结合和转化的数学思想，属于中档题．