题目内容
若函数 的两个零点是2和3,则函数
的两个零点是2和3,则函数 的零点是( )
的零点是( )
A.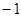 和 和 | B. 和 和 | C. 和 和 | D. 和 和 |
D
解析试题分析:因为 的零点是2,3,所以a=5,b=-6,从而
的零点是2,3,所以a=5,b=-6,从而 =
= ,其零点为
,其零点为 和
和 ,故选D。
,故选D。
考点:本题主要考查函数零点的概念,韦达定理的应用。
点评:简单题,利用韦达定理可得a,b的关系,从而通过解方程得到 的零点。
的零点。

练习册系列答案
相关题目
已知函数 是
是 上的增函数,那么实数
上的增函数,那么实数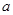 的范围( )
的范围( )
A. | B. | C. | D. |
一次函数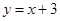 与
与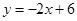 的图象的交点组成的集合是( )
的图象的交点组成的集合是( )
A. | B. | C. | D. |
甲、乙两人在一次赛跑中,从同一地点出发,路程S与时间 的函数关系如图所示,则下列说法正确的是
的函数关系如图所示,则下列说法正确的是
| A.甲比乙先出发 | B.乙比甲跑的路程多 |
| C.甲、乙两人的速度相同 | D.甲比乙先到达终点 |
如果函数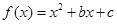 对任意实数均有
对任意实数均有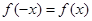 ,那么( )
,那么( )
A.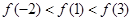 | B.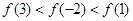 |
C.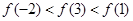 | D.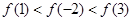 |
已知幂函数 的图象过点
的图象过点 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
若函数 在
在 上单调递增,那么实数
上单调递增,那么实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
下列说法中:
① 若 (其中
(其中 )是偶函数,则实数
)是偶函数,则实数 ;
;
②  既是奇函数又是偶函数;
既是奇函数又是偶函数;
③ 函数 的减区间是
的减区间是 ;
;
④ 已知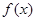 是定义在
是定义在 上的不恒为零的函数,且对任意的
上的不恒为零的函数,且对任意的 都满足
都满足 ,则
,则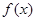 是奇函数。
是奇函数。
其中正确说法的序号是( )
| A.①②④ | B.①③④ |
| C.②③④ | D.①②③ |
已知定义在 上的函数
上的函数 满足
满足 ,且
,且 ,
,  ,若有穷数列
,若有穷数列 (
( )的前
)的前 项和等于
项和等于 ,则
,则 等于( )
等于( )
| A.4 | B.5 | C.6 | D.7 |