题目内容
19．在矩形ABCD中，AB=3，BC=4，PA⊥平面ABCD，且PA=1，PE⊥DB，垂足为E．则PE的长为$\frac{13}{5}$．分析 连接AE，则PE为点P到对角线BD的距离，即可得出结论．
解答 
解：如图所示，连接AE，则AE⊥BD
∵PE⊥DB，垂足为E，
∴PE为点P到对角线BD的距离，
∵矩形ABCD，AB=3，BC=4，
∴3×4=5×AE
∴AE=$\frac{12}{5}$
又∵PA=1，PA⊥矩形ABCD
∴PE=$\sqrt{1+（\frac{12}{5}）^{2}}$=$\frac{13}{5}$．
故答案为：$\frac{13}{5}$．
点评 本题考查空间距离，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
9．下列函数中，与函数f（x）=lnx有相同定义域的是（ ）
| A． | f（x）=$\frac{1}{\sqrt{x}}$ | B． | f（x）=$\sqrt{x}$ | C． | f（x）=|x| | D． | f（x）=2x |
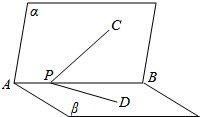如图，平面α⊥平面β，平面α∩平面β=AB，P∈AB，C∈α，D∈β，且∠CPB=∠DPB=45°，则∠CPD=60°．
如图为一半径是3米的水轮，水轮圆心O距离水面2米，开始旋转时水轮上的点P在P0位置，P0距离水面3米，已知水轮每分钟旋转4圈，求点P到水面的距离y（米）与时间x（秒）的函数关系式．