题目内容
2.若α为锐角(单位为弧度),试利用单位圆及三角函数线,比较α、sinα、tanα之间的大小关系.分析 由题意作出三角函数线,进而比较S△AOP,S扇形AOP,S△AOT的大小,可得答案.
解答 解:在直角坐标系中结合单位圆作出锐角α的正弦线和正切线,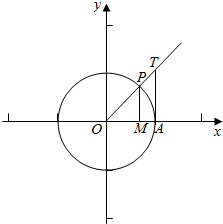
由图可知sinα=MP,α=$\widehat{AP}$,tanα=AT,
∵S△AOP=$\frac{1}{2}$×MP×1=$\frac{1}{2}$sinα,
S扇形AOP=$\frac{1}{2}$×$\widehat{AP}$×1=$\frac{1}{2}$α,
S△AOT=$\frac{1}{2}$×AT×1=$\frac{1}{2}$tanα,
∵S△AOP<S扇形AOP<S△AOT,
∴MP<$\widehat{AP}$<AT,
即sinα<α<tanα,
点评 本题考查单位圆与三角函数线,难度不大,属基础题

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
10.现有一段长为18m的铁丝,要把它围成一个底面一边长为另一边长2倍的长方体形状的框架,当长方体体积最大时,底面的较短边长是( )
| A. | 1 m | B. | 1.5 m | C. | 0.75 m | D. | 0.5 m |
17.如图所示是水平放置的三角形的直观图,AB与y轴平行,AB=OA,则三角形AOB是( )
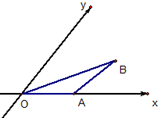

| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
11.设m、n是两条不同的直线,α、β是两个不重合的平面,则下列命题中正确的是( )
| A. | 若m∥α,m∥n,则n∥α | B. | 若m⊥α,n⊥β,则m⊥n | C. | 若m⊥α,m∥β,则α⊥β | D. | 若α⊥β,n?α,则n⊥β |