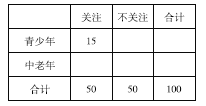
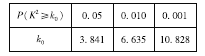
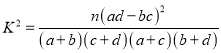题目内容
【题目】关于x的方程22x﹣(m﹣1)2x+2=0在x∈[0,2]时有唯一解,求m取值范围.
【答案】解:令2x=t,则t∈[1,4], ∴方程t2﹣(m﹣1)t+2=0在[1,4]上有唯一解.
①若△=(m﹣1)2﹣8=0,即m=1±2 ![]() 时,
时,
若m=1+2 ![]() ,则t=
,则t= ![]() ,符合题意,
,符合题意,
若m=1﹣2 ![]() ,则t=﹣
,则t=﹣ ![]() ,不符合题意.
,不符合题意.
②若△=(m﹣1)2﹣8>0,即m<1﹣2 ![]() 或m>1+2
或m>1+2 ![]() 时,
时,
若t=1是方程的解,由根与系数的关系可知t=2也是方程的解,与方程在[1,4]上有唯一解矛盾;
若t=4是方程的解,由根与系数的关系可知t= ![]() 也是方程的解,符合题意;
也是方程的解,符合题意;
此时m﹣1=4+ ![]() ,∴m=
,∴m= ![]() .
.
若方程的解在(1,4)上,根据零点的存在性定理可知(4﹣m)(22﹣4m)<0,
解得4<m< ![]() .
.
综上,m的取值范围是(4, ![]() ]∪{1+2
]∪{1+2 ![]() }
}
【解析】令2x=t,在方程t2﹣(m﹣1)t+2=0在[1,4]上有唯一解,对判别式和区间端点值进行讨论,利用二次函数的性质和零点的存在性定理得出a的范围.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目