题目内容
设函数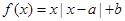 ,
,
(1)若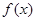 是奇函数,求a、b满足的条件;
是奇函数,求a、b满足的条件;
(2)若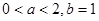 ,求
,求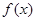 在区间[0,2]上的最大值
在区间[0,2]上的最大值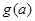 ;
;
(3)求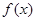 的单调区间.
的单调区间.
【答案】
(1)a=0且b=0
(2)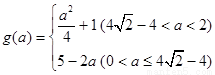
(3)单增区间有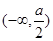 和
和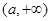 ,单减区间有
,单减区间有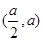
【解析】第一问中因为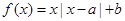 ,且
,且 是奇函数,所以f(0)=0
是奇函数,所以f(0)=0
第二问中,由图像,最大值只能在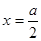 和
和 处取到
处取到
然后比较大小,确定最值。
第三问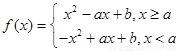 ,对于参数a进行讨论得到单调区间。
,对于参数a进行讨论得到单调区间。
解:(1解:因为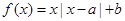 ,且
,且 是奇函数,所以f(0)=0
是奇函数,所以f(0)=0
a=0且b=0 -----------4
(2)由图像,最大值只能在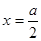 和
和 处取到
处取到
若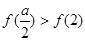 即
即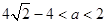 时,最大值
时,最大值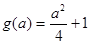
若 即
即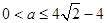 时,最大值
时,最大值
所以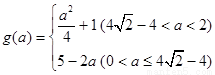 --------------10
--------------10
(3)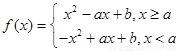
①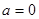 ,
,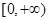
 单调递增,
单调递增, 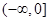
 单调递增,所以在R上单调递增
单调递增,所以在R上单调递增
②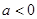 时
时
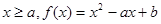 对称轴
对称轴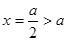 ,所以f(x)在
,所以f(x)在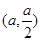 上单调减,f(x)在
上单调减,f(x)在 单调递增
单调递增
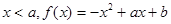 对称轴
对称轴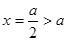 ,所以f(x)在
,所以f(x)在 上单调增
上单调增
所以,单增区间有 和
和 ,单减区间有
,单减区间有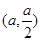
③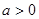 时
时
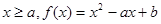 对称轴
对称轴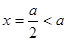 ,所以f(x)在
,所以f(x)在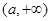 单调递增
单调递增
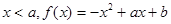 对称轴
对称轴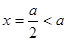 ,所以f(x)在
,所以f(x)在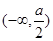 上单调增,f(x)在
上单调增,f(x)在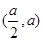 单调递减
单调递减
所以,单增区间有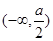 和
和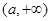 ,单减区间有
,单减区间有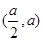 --------------16
--------------16

练习册系列答案
相关题目
 ,
,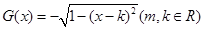
 是常数,问当
是常数,问当 有最大值,并求出
有最大值,并求出 的值;
的值; 同时满足条件:(甲)
同时满足条件:(甲) 取最小值的
取最小值的 ?
? ,求使
,求使 的
的 的取值范围.
的取值范围.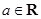 ,函数
,函数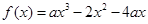 ,
, 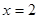 是函数
是函数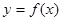 的极值点,求
的极值点,求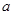 的值;
的值;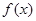 在区间
在区间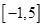 上的最值.
上的最值.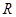 上为单调函数,若是,求出
上为单调函数,若是,求出 ,
,
 是偶函数,求
是偶函数,求 的值。
的值。 ,
, ,求
,求 的最小值。
的最小值。