题目内容
四个函数:①f(x)=
| 1 | x |
②g(x)=sinx;
③f(x)=|x|;
④f(x)=ax3+bx2+cx+d.其中在x=0处连续的函数是
分析:先分别求出函数在x=0处左右的极限,然后判定是否相等,从而逐一确定是否在x=0处连续.
解答:解:①f(x)=
,
f(x)=+∞,
f(x)=-∞,
f(x)≠
f(x),则在x=0处不连续
②g(x)=sinx,
f(x)=0,
f(x)=0,
f(x)=
f(x),则在x=0处连续
③f(x)=|x|,
f(x)=0,
f(x)=0,
f(x)=
f(x),则在x=0处连续
④f(x)=ax3+bx2+cx+d,
f(x)=d,
f(x)=d,
f(x)=
f(x),则在x=0处连续
故答案为:②③④
| 1 |
| x |
| lim |
| x→0+ |
| lim |
| x→0- |
| lim |
| x→0+ |
| lim |
| x→0- |
②g(x)=sinx,
| lim |
| x→0+ |
| lim |
| x→0- |
| lim |
| x→0+ |
| lim |
| x→0- |
③f(x)=|x|,
| lim |
| x→0+ |
| lim |
| x→0- |
| lim |
| x→0+ |
| lim |
| x→0- |
④f(x)=ax3+bx2+cx+d,
| lim |
| x→0+ |
| lim |
| x→0- |
| lim |
| x→0+ |
| lim |
| x→0- |
故答案为:②③④
点评:本题考查函数的连续性的概念,解题时要正确理解函数的连续性,再某点处连续只需在该点处的左右极限相等即可,属于基础题.

练习册系列答案
相关题目
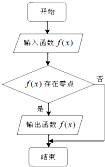 (2012•西城区二模)执行如图所示的程序框图,若输入如下四个函数:
(2012•西城区二模)执行如图所示的程序框图,若输入如下四个函数: