题目内容
已知向量 ,
, ,且
,且 .
.
(1)当 时,求
时,求 ;
;
(2)设函数 ,求函数
,求函数 的最值及相应的
的最值及相应的 的值.
的值.
(1) ;(2)当
;(2)当 时,
时, ;当
;当 时,
时, .
.
解析试题分析:(1)根据 及
及 可求得
可求得 ,即可得当
,即可得当 时,
时, ;(2)由
;(2)由 和(1)中的结论可以求得
和(1)中的结论可以求得 ,由二次函数的单调性,可以得出结论.
,由二次函数的单调性,可以得出结论.
试题解析:(1)由已知条件 ,得
,得

 ,所以,当
,所以,当 时,
时, .
. 



 ,
, 当
当 ,即
,即 时,
时, ;当
;当 ,即
,即 时,
时, .
.
考点:1.向量运算的坐标表示;2.三角恒等变换;3.函数的最值.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 中,
中, 分别为角
分别为角 的对边,
的对边, .
. 的度数;
的度数; ,求
,求 与
与 的值.
的值. 中,角
中,角 、
、 、
、 所对应的边为
所对应的边为 、
、 、
、 .
. ,求
,求 ,且
,且 ,求
,求 的值.
的值.  ,向量
,向量 ,函数
,函数 .
. 的最小正周期
的最小正周期 ;
; 分别为
分别为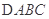 内角
内角 的对边,
的对边, 为锐角,
为锐角, ,且
,且 恰是
恰是 上的最大值,求
上的最大值,求 的值.
的值. .
. 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;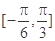 上的最大值与最小值的和为
上的最大值与最小值的和为 ,求
,求 的值.
的值. ,
, .
. 的值;
的值;  ,
, ,求
,求 .
. .
. 的最小正周期;
的最小正周期;  ,若
,若 且
且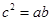 ,
, ,
, ,
, 所对的边分别为
所对的边分别为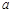 ,
, ,c.已知
,c.已知 .
. ,求T的取值范围.
,求T的取值范围. ,且
,且 为锐角,求:
为锐角,求: 的值;
的值; 的值.
的值.