题目内容
证明函数
在[-2，+∞）上是增函数．
【答案】分析：本题考查的是函数单调性的问题．在解答时要根据函数单调性的定义，先在所给的区间上任设两个数并规定大小，然后通过作差法即可分析获得两数对应函数值之间的大小关系，结合定义即可获得问题的解答．
解答：证明：任取x1，x2∈[-2，+∞），且x1＜x2，
则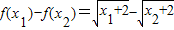
=
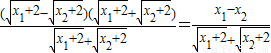
因为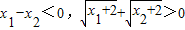
，
得f（x1）＜f（x2）
所以函数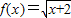
在[-2，+∞）上是增函数．
点评：本题考查的是函数单调性的问题．在解答的过程当中充分体现了函数的定义域问题、单调性判断以及作差法的技巧．值得同学们体会和反思．
解答：证明：任取x1，x2∈[-2，+∞），且x1＜x2，
则
=
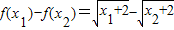
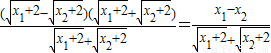
因为
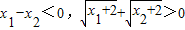，得f（x1）＜f（x2）
所以函数
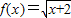在[-2，+∞）上是增函数．点评：本题考查的是函数单调性的问题．在解答的过程当中充分体现了函数的定义域问题、单调性判断以及作差法的技巧．值得同学们体会和反思．
练习册系列答案
相关题目
在[-2，+∞）上是增函数．