题目内容
若c>1,a=
-
,b=
-
.则下列结论中正确的是( )
| c |
| c-1 |
| c+1 |
| c |
| A、a>b | B、a=b |
| C、a<b | D、a≤b |
分析:由于a,b均大于0,故可利用y=
在(0,+∞)的单调递减的性质来比较大小.利用分子有理化求出a=
,b=
即可比较大小
| 1 |
| x |
| 1 | ||||
|
| 1 | ||||
|
解答:解:由于a,b均大于0,
故可利用y=
在(0,+∞)的单调递减的性质来比较大小
∵a=
-
,b=
-
.
∴a=
,,b=
∵0<
+
<
+
∴a>b
故选A
故可利用y=
| 1 |
| x |
∵a=
| c |
| c-1 |
| c+1 |
| c |
∴a=
| 1 | ||||
|
| 1 | ||||
|
∵0<
| c |
| c-1 |
| c |
| c+1 |
∴a>b
故选A
点评:本题通过研究函数的单调性来比较大小,是近几年高考长考的知识点,属于基础题.

练习册系列答案
相关题目
 如图,这是一个计算机装置示意图,A、B是数据入口处,C是计算机结果的出口,计算过程是由A、B分别输入自然数m和n,经过计算后,得自然数k,由C输出.即:f(m,n)=k,此种计算装置完成计算,满足以下三个性质:①若A、B分别输入1,则输出结果为1,即f(1,1)=1;②若A输入自然数m,B输入自然数由n变为n+1,则输出结果比原来增大2,即f(m,n+1)=f(m,n)+2;③若B输入1,A输入自然数由m变为m+1,则输出结果是原来的2倍,即f(m+1,1)=2f(m,1).
如图,这是一个计算机装置示意图,A、B是数据入口处,C是计算机结果的出口,计算过程是由A、B分别输入自然数m和n,经过计算后,得自然数k,由C输出.即:f(m,n)=k,此种计算装置完成计算,满足以下三个性质:①若A、B分别输入1,则输出结果为1,即f(1,1)=1;②若A输入自然数m,B输入自然数由n变为n+1,则输出结果比原来增大2,即f(m,n+1)=f(m,n)+2;③若B输入1,A输入自然数由m变为m+1,则输出结果是原来的2倍,即f(m+1,1)=2f(m,1).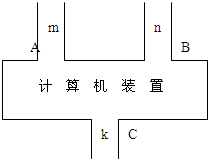 如图,这是一个计算机装置示意图,A、B是数据入口处,C是计算机结果的出口,计算过程是由A、B分别输入自然数m和n,经过计算后,得自然数k,由C输出.即:f(m,n)=k,此种计算装置完成计算,满足以下三个性质:①若A、B分别输入1,则输出结果为1,即f(1,1)=1;②若A输入自然数m,B输入自然数由n变为n+1,则输出结果比原来增大2,即f(m,n+1)=f(m,n)+2;③若B输入1,A输入自然数由m变为m+1,则输出结果是原来的2倍,即f(m+1,1)=2f(m,1).
如图,这是一个计算机装置示意图,A、B是数据入口处,C是计算机结果的出口,计算过程是由A、B分别输入自然数m和n,经过计算后,得自然数k,由C输出.即:f(m,n)=k,此种计算装置完成计算,满足以下三个性质:①若A、B分别输入1,则输出结果为1,即f(1,1)=1;②若A输入自然数m,B输入自然数由n变为n+1,则输出结果比原来增大2,即f(m,n+1)=f(m,n)+2;③若B输入1,A输入自然数由m变为m+1,则输出结果是原来的2倍,即f(m+1,1)=2f(m,1).