题目内容
f（x）在x0处可导，a为常数，则
=（ ）
| lim |
| △x→0 |
| f(x0+a△x)-f(x0-a△x) |
| △x |
| A、f′（x0） |
| B、2af′（x0） |
| C、af′（x0） |
| D、0 |
考点：变化的快慢与变化率
专题：导数的概念及应用
分析：利用导数的定义即可得出．
解答：
解：
=2a
=2af′（x0）．
故选：B．
| lim |
| △x→0 |
| f(x0+a△x)-f(x0-a△x) |
| △x |
| lim |
| △x→0 |
| f(x0+a△x)-f(x0-a△x) |
| 2a△x |
故选：B．
点评：本题考查了导数的定义，属于基础题．
练习册系列答案
相关题目
认真阅读如图所示程序框图，则输出的S等于（ ）
| A、14 | B、20 | C、30 | D、55 |
设变量x，y满足约束条件
，则z=2x+y的最大值为（ ）
|
| A、-3 | ||
B、
| ||
| C、6 | ||
| D、10 |
执行如图所示的程序框图，若输入n的值为7，则输出的s的值为（ ）
| A、22 | B、16 | C、15 | D、11 |
下面程序输出结果是（ ）
| A、1，1 | B、2，1 |
| C、1，2 | D、2，2 |
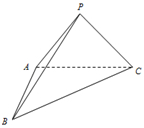如图，在三棱锥P-ABC中，AB⊥AC，PA=PB=PC=3，AB=2