题目内容
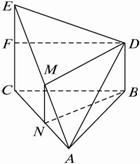
如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥EC,且EC=AC=2BD,M是AE的中点.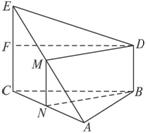
求证:(1)DE=AD;
(2)平面BDM⊥平面ECA.
思路点拨:(1)要证明DE=AD,只需要证明Rt△DFE≌Rt△ABD;(2)注意点M为EA的中点,可取AC的中点N,先证明点N在平面BDM内,再证明平面BDM经过平面ECA的一条垂线即可.
证明:(1)取EC的中点F,连结DF.
∵EC⊥BC,易知DF∥BC,∴DF⊥EC.
在Rt△DFE和Rt△ABD中,FE=![]() EC=BD,DF=BC=AB,∴Rt△DFE≌Rt△ABD.故DE=AD.
EC=BD,DF=BC=AB,∴Rt△DFE≌Rt△ABD.故DE=AD.
(2)取AC的中点N,连结MN、BN,则MN∥EC,MN=![]() EC.
EC.
∴MN∥BD,即点N在平面BDM内.
又EC⊥平面ABC,
∴EC⊥BN.
又AC⊥BN,∴BN⊥平面ECA.
又∵平面BDM经过BN,
∴平面BDM⊥平面ECA.
[一通百通] 有关面面垂直的判定问题,通常情况下可以根据面面垂直的判定定理来考虑,将问题转化为证明线面垂直,从而将问题证明.

练习册系列答案
相关题目
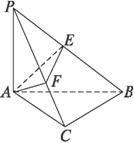
 的交线, 已知二面角
的交线, 已知二面角 为直二面角,
为直二面角, 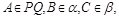
 , ∠BAP=45°.
, ∠BAP=45°. 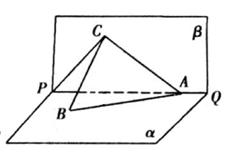
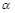 内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心?
内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心? 时, 求二面角B-AC-P的大小.
时, 求二面角B-AC-P的大小.