题目内容
5.已知函数f(x)=x•sinx,有下列四个结论:①函数f(x)的图象关于y轴对称;
②存在常数T>0,对任意的实数x,恒有f(x+T)=f(x);
③对于任意给定的正数M,都存在实数x0,使得|f(x0)|≥M;
④函数f(x)在[0,π]上的最大值是$\frac{π}{2}$.
其中正确结论的序号是①③(请把所有正确结论的序号都填上).
分析 ①研究函数的奇偶性,可用偶函数的定义来证明之;
②研究的是函数的周期性,采用举对立面的形式说明其不成立;
③找出一个常数M,都存在实数x0,使得|f(x0)|≥M成立即可;
④根据f($\frac{π}{2}$)=$\frac{π}{2}$,$\frac{π}{2}$不是函数的极值点,即可得出结论.
解答 解:对于①,∵f(-x)=-x•sin(-x)=xsinx=f(x),∴函数为偶函数,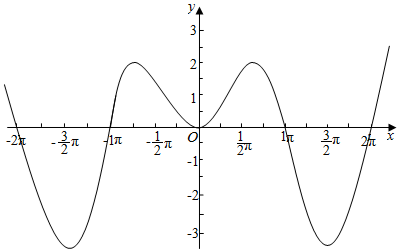
∴函数f(x)的图象关于y轴对称,故①正确;
对于②∵当x=2kπ+$\frac{π}{2}$时,f(x)=x,随着x的增大函数值也在增大,所以不会是周期函数,故②错;
对于③∵|sinx0|≤1,∴对任意给定的正数M,都存在实数x0,使得|f(x0)|≥M,故③正确;对于④,f($\frac{π}{2}$)=$\frac{π}{2}$.∵f′(x)=sinx+xcosx,∴f′($\frac{π}{2}$)=1,∴$\frac{π}{2}$不是函数的极值点,故④不正确
故答案为:①③.
点评 本题考点是函数的单调性判断与证明,函数的奇偶性,函数的中心对称的判断及函数的周期性,涉及到的性质比较多,且都是定义型,本题知识性较强,做题时要注意准确运用相应的知识准确解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.现有三所大学正在进行自主招生,甲,乙两位同学各自选报其中一所大学,每位同学选报各个大学的可能性相同,则这两位同学选报同一所大学的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
13.设Sn是公差d≠0的等差数列{an}的前n项和,且S1,S2,S4成等比数列,则$\frac{{S}_{3}}{{a}_{3}}$=( )
| A. | $\frac{9}{5}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | 2 |
 如图程序框图的算法思路源于世界数学名题“3x+1问题”.执行该程序框图,若输入的N=3,则输出i=( )
如图程序框图的算法思路源于世界数学名题“3x+1问题”.执行该程序框图,若输入的N=3,则输出i=( )