题目内容
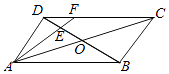
【题目】在平行四边形ABCD中，AC与BD交于点O，E是线段OD的中点，AE的延长线与CD相交于点F．若AB=2， 
，∠BAD=45°，则 
=（ ）
A.
B.1
C.﹣
D.1
【答案】C
【解析】解：平行四边形ABCD，AB=2， 
，∠BAD=45°，DF∥AB，
可得△DEF∽△BEA，
E是线段OD的中点，
可得DF：BA═DE：BE=EF：AE=1：3，
= 
= 
× 
（ 
+ 
）= 
（ 
+ 
+ ）
= （ + 
）；
= 
= 
（ ﹣ 
），
则 
= （ + ）（ ﹣ ）
= （ 
2﹣ 2﹣ ）= ×（ 
×2﹣ ×4﹣2 
× 
）
=﹣ ．
所以答案是：C．
【考点精析】本题主要考查了向量的三角形法则的相关知识点，需要掌握三角形加法法则的特点：首尾相连;三角形减法法则的特点：共起点，连终点，方向指向被减向量才能正确解答此题．
小学课堂作业系列答案
金博士一点全通系列答案
【题目】某大学为调研学生在A，B两家餐厅用餐的满意度，从在A，B两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行评分，满分均为60分．整理评分数据，将分数以10为组距分成6组：[0，10），[10，20），[20，30），[30，40），[40，50），[50，60]，得到A餐厅分数的频率分布直方图，和B餐厅分数的频数分布表：
B餐厅分数频数分布表 | |
分数区间 | 频数 |
[0，10） | 2 |
[10，20） | 3 |
[20，30） | 5 |
[30，40） | 15 |
[40，50） | 40 |
[50，60] | 35 |
定义学生对餐厅评价的“满意度指数”如下：
分数 | [0，30） | [30，50） | [50，60] |
满意度指数 | 0 | 1 | 2 |
（Ⅰ）在抽样的100人中，求对A餐厅评价“满意度指数”为0的人数；
（Ⅱ）从该校在A，B两家餐厅都用过餐的学生中随机抽取1人进行调查，试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率；
（Ⅲ）如果从A，B两家餐厅中选择一家用餐，你会选择哪一家？说明理由．
