题目内容
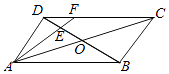
【题目】如图,A、B是海面上两个固定观测站,现位于B点南偏东45°且相距 ![]() 海里的D处有一艘轮船发出求救信号.此时在A处观测到D位于其北偏东30°处,位于A北偏西30°且与A相距
海里的D处有一艘轮船发出求救信号.此时在A处观测到D位于其北偏东30°处,位于A北偏西30°且与A相距 ![]() 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
【答案】解:由题意,BD=5 ![]() ,AC=20
,AC=20 ![]() ,∠BAD=30°,∠ABD=45°,
,∠BAD=30°,∠ABD=45°,
∠CAD=60°
在△DAB中,由正弦定理得, ![]() =
= ![]() ,
,
∴AD= ![]() sin∠ABD=
sin∠ABD= ![]() sin45°=10
sin45°=10 ![]() ,
,
在△ACD中,由余弦定理得CD2=AD2+AC2﹣2ACADcos∠CAD=
(20 ![]() )2+(10
)2+(10 ![]() )2﹣2×20×10
)2﹣2×20×10 ![]() ×
× ![]() =900,
=900,
∴CD=30,
∵航行速度为30海里/小时,
∴该救援船到达D点需要1(小时).
答:救援船到达D点需要1小时
【解析】在![]() 中根据正弦定理可知
中根据正弦定理可知![]() =
=![]() ,从而求出AD;在
,从而求出AD;在![]() 中根据余弦定理可知CD2=AD2+AC2-2AC
中根据余弦定理可知CD2=AD2+AC2-2AC![]() AD
AD![]() cos
cos![]() ,从而求出CD.
,从而求出CD.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目