Question

【题目】如图，在平面直角坐标系xoy中，A为以原点O为圆心的单位圆O与x正半轴的交点，在圆心角为 的扇形AOB的弧AB上任取一点 P，作 PN⊥OA于N，连结PO，记∠PON=θ．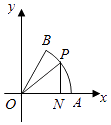
（1）设△PON的面积为y，使y取得最大值时的点P记为E，点N记为F，求此时 的值；
（2）求k=a| || |+ （a∈R，E 是在（1）条件下的点 E）的值域．

Answer 1

【答案】
（1）解：ON=cosθ，PN=sinθ，

∴y= cosθsinθ= sin2θ，

∵0 ，

∴当 时，y取得最大值，此时E（ ， ），F（ ，0），

∴ = ．

（2）解： =（cosθ，sinθ）， =（ ， ），

∴ = cosθ+ sinθ= （sinθ+cosθ），

∴k=asinθcosθ+sinθ+cosθ，

令sinθ+cosθ= sin（ ）=t，则sinθcosθ= ，

∵0 ，∴ ≤ ，

∴1＜t ，

∴k=a +t= ，

令f（t）= ，

①若a=0，则f（t）=t，∴f（t）的值域为（1， ]；

②若a＞0，则f（t）的对称轴为直线x=﹣ ＜0，

∴f（t）在（1， ]上单调递增，

∴f（1）＜f（t）≤f（ ），即f（t）的值域为（1， + ]；

③若a＜0，则f（t）的图象开口向下，

若﹣ ≤1，即a≤﹣1时，f（t）在（1， ]上单调递减，

∴f（t）的值域为[ + ，1）；

若﹣ ≥ ，即﹣ ≤a＜0时，f（t）在（1， ]上单调递增，

∴f（t）的值域为（1， + ]；

若1＜﹣ ，即﹣1 时，f（t）在（1， ]上先增后减，

∴f（t）的最大值为f（﹣ ）= ，

若1 ＜ ，即﹣1＜a＜2﹣2 时，则f（t）的最小值为f（ ）= ，

若 ≤﹣ ，即2﹣2 ≤a＜﹣ 则f（t）的最小值为f（1）=1，

综上，当a=0时，f（t）的值域为（1， ]；

当a≤﹣1时，k的值域是[ + ，1）；

当a＞﹣ 且a≠0时，k的值域是（1， + ]；

﹣1＜a＜2﹣2 时，k的值域是[ ， ]；

当2﹣2 ≤a＜﹣ 时，k的值域是（1， ]．

【解析】（1）用θ表示出PN，ON，得出y关于θ的函数，利用正弦函数的性质得出y最大时对应的θ值，从而求出E，F的坐标，再计算 ；（2）设sinθ+cosθ=t，得出k关于t的函数，讨论a的取值与函数单调性，得出k的值域．