题目内容
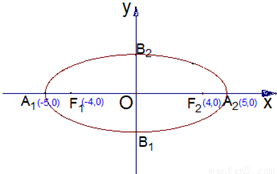
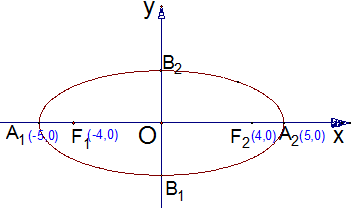 如图,A1,A为椭圆的两个顶点,F1,F2为椭圆的两个焦点.
如图,A1,A为椭圆的两个顶点,F1,F2为椭圆的两个焦点.(Ⅰ)写出椭圆的方程;
(Ⅱ)过线段OA上异于O,A的任一点K作OA的垂线,交椭圆于P,P1两点,直线A1P与AP1交于点M.求证:点M在双曲线
| x2 |
| 25 |
| y2 |
| 9 |
分析:(Ⅰ)根据椭圆顶点,焦点坐标,可得a,c的值,从而可求b的值,即可得到椭圆的方程;
(Ⅱ)设K点坐标,表示出直线A1P,P1A的方程,求出直线A1P与AP1的交点M的坐标,代入双曲线方程,即可得到结论.
(Ⅱ)设K点坐标,表示出直线A1P,P1A的方程,求出直线A1P与AP1的交点M的坐标,代入双曲线方程,即可得到结论.
解答:(Ⅰ)解:由图可知,a=5,c=4,∴b=
=3.
∴该椭圆的方程为
+
=1,
(Ⅱ)证明:设K点坐标(x0,0),点P、P1的坐标分别记为(x0,y0),(x0,-y0),
其中0<x0<5,则
+
=1,…①
直线A1P,P1A的方程分别为:(x0+5)y=y0(x+5),…②(5-x0)y=y0(x-5).…③
②式除以③式得
=
,化简上式得x=
,代入②式得y=
,
于是,直线A1P与AP1的交点M的坐标为(
,
).
因为
(
)2-
(
)2=
-
(1-
)=1.
所以,直线A1P与AP1的交点M在双曲线
-
=1上.
| a2-c2 |

∴该椭圆的方程为
| x2 |
| 25 |
| y2 |
| 9 |
(Ⅱ)证明:设K点坐标(x0,0),点P、P1的坐标分别记为(x0,y0),(x0,-y0),
其中0<x0<5,则
| ||
| 25 |
| ||
| 9 |
直线A1P,P1A的方程分别为:(x0+5)y=y0(x+5),…②(5-x0)y=y0(x-5).…③
②式除以③式得
| x0+5 |
| 5-x0 |
| x+5 |
| x-5 |
| 25 |
| x0 |
| 5y0 |
| x0 |
于是,直线A1P与AP1的交点M的坐标为(
| 25 |
| x0 |
| 5y0 |
| x0 |
因为
| 1 |
| 25 |
| 25 |
| x0 |
| 1 |
| 9 |
| 5y0 |
| x0 |
| 25 | ||
|
| 25 | ||
|
| ||
| 25 |
所以,直线A1P与AP1的交点M在双曲线
| x2 |
| 25 |
| y2 |
| 9 |
点评:本题考查椭圆的标准方程,考查直线的交点,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
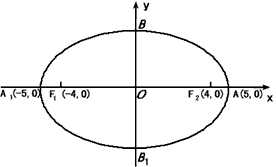
 (2003•北京)如图,A1,A为椭圆的两个顶点,F1,F2为椭圆的两个焦点.
(2003•北京)如图,A1,A为椭圆的两个顶点,F1,F2为椭圆的两个焦点.
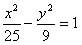 上。
上。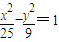 上.
上.