题目内容
((本小题14分)
已知函数
(I)若函数 在
在 时取得极值,求实数
时取得极值,求实数 的值;
的值;
(II)试讨论函数 的单调性;
的单调性;
 (
( ) ……………………………1分
) ……………………………1分
(I)∵函数 在
在 时取到极值
时取到极值
∴ 解得
解得
经检验 函数
函数 在
在 时取到极小值(不检验扣1分)
时取到极小值(不检验扣1分)
∴实数 的值-2
的值-2  …………………………4分
…………………………4分 (II)由
(II)由 得
得 或
或 …………………………5分
…………………………5分
①当 时,
时,
由 得
得
由 得
得
∴函数 得单调增区间为
得单调增区间为 ,单调减区间为
,单调减区间为 …………7分
…………7分
②当 时,
时, ,同理可得函数
,同理可得函数 得单调增区间为
得单调增区间为 ,
,
单调减区间为 ………………………………9分
………………………………9分
(II)假设存在满足要求的两点A,B,即在点A、B处的切线都与y轴垂直,则
即 解得
解得 或
或
∴A ,B
,B

解析

练习册系列答案
相关题目
 .
. ,点P为曲线
,点P为曲线 上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程; 上为单调增函数,试求
上为单调增函数,试求 的取值范围.
的取值范围. 满足:
满足: ,
, ,且该函数的最小值为1.
,且该函数的最小值为1. =
=  .(其中
.(其中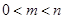 ). 问是否存在这样的两个实数
). 问是否存在这样的两个实数 ,使得函数
,使得函数
 且函数
且函数 在区间
在区间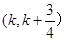 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
, ……
…… .
. ,x∈[1,+∞
,x∈[1,+∞
 时,求函数f(x)的最小值
时,求函数f(x)的最小值 
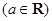 .
. ,求曲线
,求曲线 在
在 处切线的斜率;
处切线的斜率; 的单调区间;
的单调区间; ,若对任意
,若对任意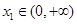 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。