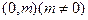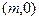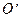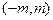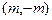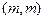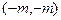题目内容
已知两点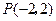 ,
,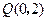 以及一条直线
以及一条直线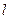 :
: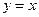 ,设长为
,设长为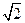 的线段
的线段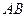 在直线
在直线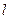 上移动,求直线
上移动,求直线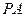 和
和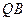 的交点
的交点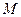 的轨迹方程.
的轨迹方程.
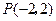 ,
,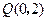 以及一条直线
以及一条直线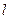 :
: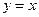 ,设长为
,设长为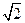 的线段
的线段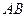 在直线
在直线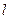 上移动,求直线
上移动,求直线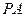 和
和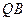 的交点
的交点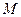 的轨迹方程.
的轨迹方程.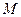 的轨迹方程为
的轨迹方程为 .
. 线段
线段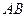 在直线
在直线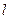 :
: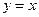 上,且线段
上,且线段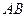 的长为
的长为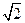 ,
, 设
设 ,
, ,
, (
( 为参数),则直线
为参数),则直线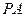 的方程为
的方程为 , ①
, ①直线
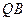 的方程为
的方程为 . ②
. ② 是直线
是直线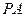 ,
,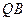 的交点,
的交点, ,
, 是由①,②组成的方程组的解,由①,②消去参数
是由①,②组成的方程组的解,由①,②消去参数 ,
,得
 . ③
. ③当
 时,
时,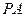 的方程为
的方程为 ,
,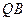 的方程为
的方程为 ,此时的交点为
,此时的交点为 .
.当
 时,
时,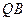 的方程为
的方程为 ,
,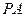 的方程为
的方程为 ,此时的交点为
,此时的交点为 .
.经验证,点
 和
和 均满足方程③.
均满足方程③.故点
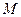 的轨迹方程为
的轨迹方程为 .
.
练习册系列答案
相关题目
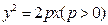 的焦点
的焦点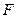 作互相垂直的两条直线,分别交准线于
作互相垂直的两条直线,分别交准线于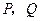 两点,又过
两点,又过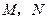 两点,求证
两点,求证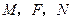 三点共线.
三点共线.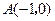 ,点
,点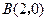 ,在第一象限的动点
,在第一象限的动点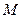 满足
满足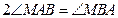 ,求点
,求点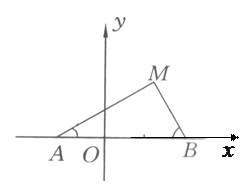
 的准线与
的准线与 轴的交点为
轴的交点为 ,过点
,过点 交抛物线于
交抛物线于 两点,若线段
两点,若线段 的垂直平分线交对称轴于
的垂直平分线交对称轴于 ,求证:
,求证: ;
;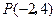 ,倾斜角为
,倾斜角为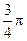 的直线
的直线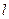 与抛物线
与抛物线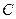 相交于
相交于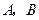 两点,抛物线
两点,抛物线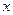 轴为对称轴,若
轴为对称轴,若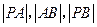 成等比数列,求抛物线
成等比数列,求抛物线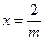
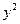 (
(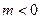 )与椭圆
)与椭圆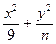 =1有一个相同的焦点,则动点
=1有一个相同的焦点,则动点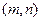 的轨迹是( )
的轨迹是( ) 双曲线的一部分
双曲线的一部分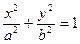 过定点A(1,0),且焦点在x轴上,椭圆与曲线|y|=x的交点为B、C。现有以A为焦点,过点B、C且开口向左的抛物线,抛物线的顶点坐标为M(m,0)。当椭圆的离心率e满足
过定点A(1,0),且焦点在x轴上,椭圆与曲线|y|=x的交点为B、C。现有以A为焦点,过点B、C且开口向左的抛物线,抛物线的顶点坐标为M(m,0)。当椭圆的离心率e满足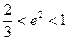 时,求实数m的取值范围。
时,求实数m的取值范围。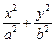 =1(a>b>0)与直线l: x+y=1在第一象限内有两个不同的交点,求a、b所满足的条件,并画出点P(a,b)的存在区域.
=1(a>b>0)与直线l: x+y=1在第一象限内有两个不同的交点,求a、b所满足的条件,并画出点P(a,b)的存在区域.