题目内容
 函数f(x)=asin
函数f(x)=asin (A>0,w>0)的图象的一部分如图所示.
(A>0,w>0)的图象的一部分如图所示.
(1)求A,w的值,并写出这个函数的单调增区间;
(2)当 时,讨论函数y=f(x)与y=a(a为常数)的图象的交点的个数.
时,讨论函数y=f(x)与y=a(a为常数)的图象的交点的个数.
解:(1)由图象可知A=2,T=π;
所以ω=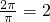
所以f(x)=2sin(2x+ );它的单调增区间为:[k
);它的单调增区间为:[k ,k
,k ]k∈Z
]k∈Z
(2)f(x)=2sin(2x+ )在区间
)在区间 上是单调减函数,
上是单调减函数,
在区间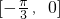 是单调增函数,
是单调增函数,
x∈ 时,f(x)∈[-2,-1]
时,f(x)∈[-2,-1]
x∈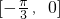 时f(x)∈[-2,1]
时f(x)∈[-2,1]
当-2<a≤-1时函数y=f(x)与y=a(a为常数)的图象的交点的个数为:2;
当-2=a或-1<a≤1时函数y=f(x)与y=a(a为常数)的图象的交点的个数为:1;
当1<a或a<-2时函数y=f(x)与y=a(a为常数)的图象的交点的个数为:0;
分析:(1)通过函数的图象,求出A,T,转化为ω,得到函数的解析式,直接求出单调增区间即可.
(2)当 时,求出函数的最值,以及函数的值域,利用单调性,说明函数y=f(x)与y=a(a为常数)的图象的交点的个数.
时,求出函数的最值,以及函数的值域,利用单调性,说明函数y=f(x)与y=a(a为常数)的图象的交点的个数.
点评:本题是基础题,考查三角函数的基本知识,考查视图能力,利用基本函数的基本性质,考查分析问题解决问题的能力.
所以ω=
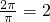
所以f(x)=2sin(2x+
 );它的单调增区间为:[k
);它的单调增区间为:[k ,k
,k ]k∈Z
]k∈Z(2)f(x)=2sin(2x+
 )在区间
)在区间 上是单调减函数,
上是单调减函数,在区间
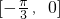 是单调增函数,
是单调增函数,x∈
 时,f(x)∈[-2,-1]
时,f(x)∈[-2,-1]x∈
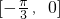 时f(x)∈[-2,1]
时f(x)∈[-2,1]当-2<a≤-1时函数y=f(x)与y=a(a为常数)的图象的交点的个数为:2;
当-2=a或-1<a≤1时函数y=f(x)与y=a(a为常数)的图象的交点的个数为:1;
当1<a或a<-2时函数y=f(x)与y=a(a为常数)的图象的交点的个数为:0;
分析:(1)通过函数的图象,求出A,T,转化为ω,得到函数的解析式,直接求出单调增区间即可.
(2)当
 时,求出函数的最值,以及函数的值域,利用单调性,说明函数y=f(x)与y=a(a为常数)的图象的交点的个数.
时,求出函数的最值,以及函数的值域,利用单调性,说明函数y=f(x)与y=a(a为常数)的图象的交点的个数.点评:本题是基础题,考查三角函数的基本知识,考查视图能力,利用基本函数的基本性质,考查分析问题解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,是函数f(x)=Asin(φx+φ)(其中A>0,φ>0,0<φ<π)的部分图象,则其解析为
如图,是函数f(x)=Asin(φx+φ)(其中A>0,φ>0,0<φ<π)的部分图象,则其解析为 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<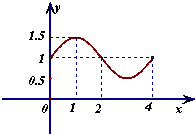 函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2008)的值分别为( )
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2008)的值分别为( )