题目内容
【题目】一根水平放置的长方体形枕木的安全负荷与它的宽度![]() 成正比,与它的厚度
成正比,与它的厚度![]() 的平方成正比,与它的长度
的平方成正比,与它的长度![]() 的平方成反比.
的平方成反比.
(Ⅰ)将此枕木翻转90°(即宽度变为厚度),枕木的安全负荷会如何变化?为什么?(设翻转前后枕木的安全负荷分别为![]() 且翻转前后的比例系数相同都为
且翻转前后的比例系数相同都为![]() )
)
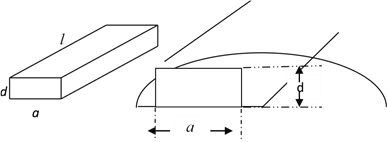
(Ⅱ)现有一根横断面为半圆(已知半圆的半径为![]() )的木材,用它来截取成长方体形的枕木,其长度为10,问截取枕木的厚度为
)的木材,用它来截取成长方体形的枕木,其长度为10,问截取枕木的厚度为![]() 多少时,可使安全负荷
多少时,可使安全负荷![]() 最大?
最大?
【答案】(Ⅰ) 见解析 (Ⅱ) ![]()
【解析】试题分析:(1)安全负荷![]() 为正常数),翻转
为正常数),翻转![]() 后
后![]() ,从而得
,从而得![]() ,从而讨论变化;(2)如图,设截取的宽为
,从而讨论变化;(2)如图,设截取的宽为![]() ,厚度为
,厚度为![]() ,则
,则![]() ,即
,即![]() ,从而得到
,从而得到 ,再求导
,再求导![]() ,确定函数的单调性与最值.
,确定函数的单调性与最值.
试题解析:(Ⅰ)安全负荷![]() 为正常数)翻转
为正常数)翻转![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 安全负荷变大.
安全负荷变大.
当 ![]() ,安全负荷变小;
,安全负荷变小;
当![]() 时,
时,![]() 安全负荷不变.
安全负荷不变.
(II)如图,设截取的宽为![]() ,厚度为
,厚度为![]() ,则
,则![]() .
.
![]()
![]() =
=![]() (
(![]()
![]()
![]() 令
令![]() 得:
得: ![]()
当![]() 时
时 ![]() 函数
函数![]() 在
在![]() 上为增函数;
上为增函数;
当![]() 时
时 ![]() 函数
函数![]() 在
在![]() 上为减函数;
上为减函数;
当 ![]() 时,安全负荷
时,安全负荷![]() 最大。此时厚度
最大。此时厚度![]()
答:当问截取枕木的厚度为![]() 时,可使安全负荷最大。
时,可使安全负荷最大。

练习册系列答案
相关题目
【题目】为了了解青少年的肥胖是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:
常喝 | 不常喝 | 总计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
总计 | 30 |
已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为![]() .
.
(1)请将列联表补充完整;(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
独立性检验临界值表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.