题目内容
17．函数y=$\frac{2-{x}^{2}}{2+{x}^{2}}$的值域为[-1，1]．分析 分离常数可得y=-1+$\frac{4}{2+{x}^{2}}$，由2+x2≥2和不等式的性质可得．
解答 解：分离常数可得y=$\frac{2-{x}^{2}}{2+{x}^{2}}$=$\frac{-（2+{x}^{2}）+4}{2+{x}^{2}}$=-1+$\frac{4}{2+{x}^{2}}$，
∵2+x2≥2，∴0＜$\frac{4}{2+{x}^{2}}$≤2，∴-1＜-1+$\frac{4}{2+{x}^{2}}$≤1，
∴原函数的值域为：[-1，1]
故答案为：[-1，1]
点评 本题考查函数的值域，涉及分离常数法和不等式的性质，属基础题．
练习册系列答案
计算高手系列答案
相关题目
7．设f（x）=xsinx，x∈$[{-\frac{π}{2}，\frac{π}{2}}]$，若f（x1）＞f（x2），则下列不等式中必定成立的是（ ）
| A． | x1-x2＜0 | B． | x1-x2＞0 | C． | x12-x22＞0 | D． | x12＜x22 |
8．扇形的半径是6cm，圆心角为15°，则扇形面积是（ ）
| A． | $\frac{π}{2}c{m^2}$ | B． | 3πcm2 | C． | πcm2 | D． | $\frac{3π}{2}c{m^2}$ |
2．设f（x）是定义在（-∞，+∞）上的减函数，且x1+x2＞0，则（ ）
| A． | f（x1）＞f（-x2） | B． | f（-x1）＞f（-x2） | C． | f（x1）＜f（-x2） | D． | f（-x1）＜f（-x2） |
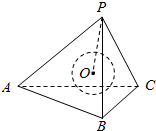正三棱锥高为1，底面边长为2$\sqrt{6}$，内有一球与四个面都相切．