题目内容
设椭圆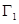 的中心和抛物线
的中心和抛物线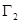 的顶点均为原点
的顶点均为原点 ,
,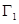 、
、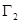 的焦点均在
的焦点均在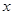 轴上,过
轴上,过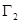 的焦点F作直线
的焦点F作直线 ,与
,与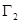 交于A、B两点,在
交于A、B两点,在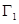 、
、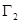 上各取两个点,将其坐标记录于下表中:
上各取两个点,将其坐标记录于下表中: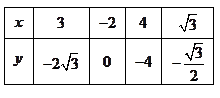
(1)求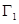 ,
,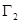 的标准方程;
的标准方程;
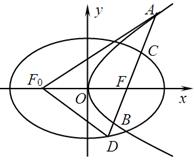
(2)若 与
与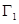 交于C、D两点,
交于C、D两点,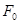 为
为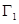 的左焦点,求
的左焦点,求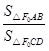 的最小值;
的最小值;
(3)点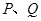 是
是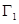 上的两点,且
上的两点,且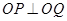 ,求证:
,求证: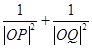 为定值;反之,当
为定值;反之,当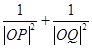 为此定值时,
为此定值时,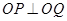 是否成立?请说明理由.
是否成立?请说明理由.
(1)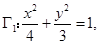

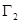 :
: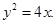 ;(2)
;(2)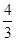 ;(3)证明见解析.
;(3)证明见解析.
解析试题分析:(1)分析哪些点在椭圆上,哪些点在抛物线上,显然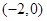 是椭圆的顶点,因此
是椭圆的顶点,因此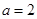 ,从而点
,从而点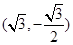 是椭圆上的点,另两点在抛物线上,代入它们的标准方程可求得其方程;(2)
是椭圆上的点,另两点在抛物线上,代入它们的标准方程可求得其方程;(2) 与
与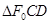 的顶点都是
的顶点都是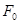 ,底在同一直线上,因此基、其面积之比为底的比,即
,底在同一直线上,因此基、其面积之比为底的比,即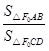
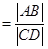 ,这样我们只要求出直线
,这样我们只要求出直线 与已知两曲线相交弦长即可,直线
与已知两曲线相交弦长即可,直线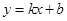 与曲线
与曲线 交于两点,其弦长为
交于两点,其弦长为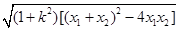 ,当然由于直线过圆锥曲线的焦点,弦长也可用焦半径公式表示;(3)从题意可看出,只有把
,当然由于直线过圆锥曲线的焦点,弦长也可用焦半径公式表示;(3)从题意可看出,只有把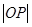 ,
,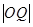 求出来,才能得出结论,为了求
求出来,才能得出结论,为了求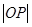 ,
,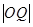 ,我们可设
,我们可设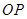 方程为
方程为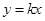 ,则
,则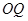 方程为
方程为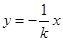 ,这样
,这样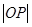 ,
,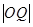 都能用
都能用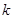 表示出来,再计算
表示出来,再计算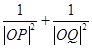 可得其为定值
可得其为定值 ,反之若
,反之若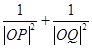
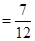 ,我们只能设
,我们只能设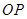 方程为
方程为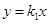 ,
,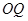 方程为
方程为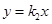 ,分别求出
,分别求出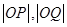 ,代入此式,得出
,代入此式,得出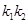 ,如果一定能得到
,如果一定能得到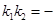 1,则就一定有
1,则就一定有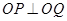 ,否则就不一定有
,否则就不一定有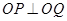 .
.
试题解析:(1)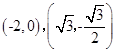 在椭圆上,
在椭圆上,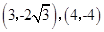 在抛物线上,
在抛物线上,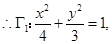

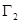 :
: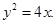 (4分)
(4分)
(2)(理)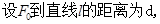
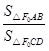 =
=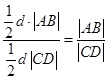 .
.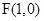 是抛物线的焦点,也是椭圆的右焦点,①当直线
是抛物线的焦点,也是椭圆的右焦点,①当直线 的斜率存在时,
的斜率存在时,
设 :
: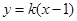 ,
,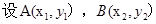 ,
,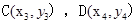
联立方程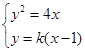 ,得
,得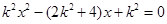 ,
,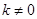 时
时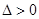 恒成立.
恒成立.
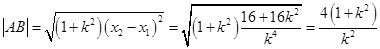
(也可用焦半径公式得: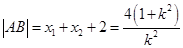 ) (5分)
) (5分)
联立方程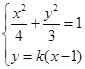 ,得
,得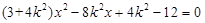 ,
,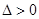 恒成立.
恒成立.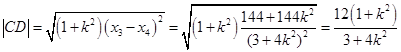 , (6分)
, (6分)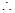
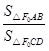 =
= . (8分)
. (8分)
②当直线 的斜率不存在时,
的斜率不存在时, :
: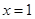 ,
,
此时,

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
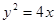 的顶点作射线
的顶点作射线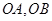 与抛物线交于
与抛物线交于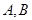 ,若
,若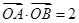 ,求证:直线
,求证:直线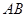 过定点.
过定点.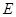 的中心在原点,焦点在
的中心在原点,焦点在 轴上,椭圆上的点到焦点的最小距离为
轴上,椭圆上的点到焦点的最小距离为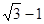 ,离心率
,离心率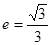 .
.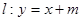 交
交 、
、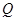 两点,点
两点,点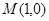 ,问是否存在
,问是否存在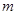 ,使
,使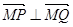 ?若存在求出
?若存在求出 的长轴长为
的长轴长为 ,离心率为
,离心率为 ,
, 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点 ,且与直线
,且与直线 相切.
相切. 的方程;(ⅱ)求动圆圆心轨迹
的方程;(ⅱ)求动圆圆心轨迹 的方程;
的方程; ,满足
,满足 与
与 共线,
共线, 与
与 共线,且
共线,且 ,求四边形
,求四边形 面积的最小值.
面积的最小值. 的离心率为
的离心率为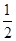 ,过椭圆右焦点
,过椭圆右焦点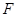 作两条互相垂直的弦
作两条互相垂直的弦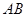 与
与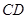 .当直线
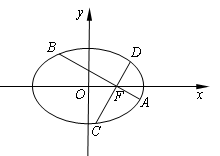
.当直线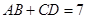 .
.
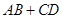 的取值范围.
的取值范围.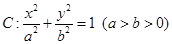 的左、右焦点分别为
的左、右焦点分别为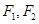 ,其上顶点为
,其上顶点为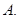 已知
已知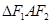 是边长为
是边长为 的正三角形.
的正三角形.
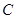 的方程;
的方程; 任作一动直线
任作一动直线 交椭圆
交椭圆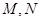 两点,记
两点,记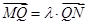 .若在线段
.若在线段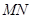 上取一点
上取一点 ,使得
,使得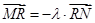 ,当直线
,当直线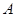 到两个定点
到两个定点 、
、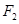 的距离之和为
的距离之和为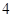 ,线段
,线段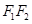 的长为
的长为
 .
.
 ;
;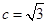 时,过点
时,过点 与轨迹
与轨迹 两点,且点
两点,且点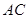 的垂直平分线为
的垂直平分线为
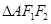 的面积的最大值;
的面积的最大值;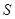 、
、 关于直线
关于直线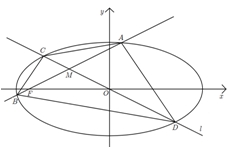
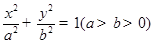 的离心率为
的离心率为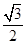 ,过左焦点
,过左焦点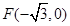 且斜率为
且斜率为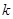 的直线交
的直线交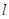 :
: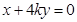 交椭圆E于C,D两点.
交椭圆E于C,D两点.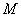 与两定点
与两定点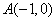 、
、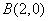 构成
构成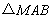 ,且
,且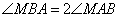 ,设动点
,设动点 .
.
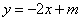 与
与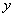 轴相交于点
轴相交于点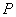 ,与轨迹
,与轨迹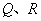 ,且
,且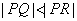 ,求
,求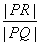 的取值范围.
的取值范围.