题目内容
已知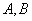 是抛物线
是抛物线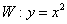 上的两个点,点
上的两个点,点 的坐标为
的坐标为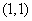 ,直线
,直线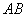 的斜率为k,
的斜率为k, 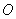 为坐标原点.
为坐标原点.
(Ⅰ)若抛物线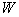 的焦点在直线
的焦点在直线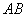 的下方,求k的取值范围;
的下方,求k的取值范围;
(Ⅱ)设C为W上一点,且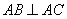 ,过
,过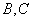 两点分别作W的切线,记两切线的交点为
两点分别作W的切线,记两切线的交点为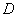 ,求
,求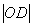 的最小值.
的最小值.
(Ⅰ)解:抛物线 的焦点为
的焦点为 .
.
由题意,得直线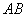 的方程为
的方程为 ,
,
令  ,得
,得 ,即直线
,即直线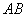 与y轴相交于点
与y轴相交于点 .
.
因为抛物线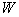 的焦点在直线
的焦点在直线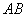 的下方,
的下方,
所以  ,
,
解得  .
.
(Ⅱ)解:由题意,设 ,
, ,
, ,
,
联立方程 消去
消去 ,得
,得 ,
,
由韦达定理,得 ,所以
,所以  .
.
同理,得 的方程为
的方程为 ,
, .
.
对函数 求导,得
求导,得 ,
,
所以抛物线 在点
在点 处的切线斜率为
处的切线斜率为 ,
,
所以切线 的方程为
的方程为 , 即
, 即 .
.
同理,抛物线 在点
在点 处的切线
处的切线 的方程为
的方程为 .
.
联立两条切线的方程
解得 ,
, ,
,
所以点 的坐标为
的坐标为 .
.
因此点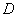 在定直线
在定直线 上.
上.
因为点 到直线
到直线 的距离
的距离 ,
,
所以 ,当且仅当点
,当且仅当点 时等号成立.
时等号成立.
由 ,得
,得 ,验证知符合题意.
,验证知符合题意.
所以当 时,
时,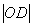 有最小值
有最小值 .
.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
 椭圆的离心率
椭圆的离心率 ,命题
,命题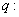 与抛物线只有一个公共点的直线是此抛物线的切线,那么 ( )
与抛物线只有一个公共点的直线是此抛物线的切线,那么 ( ) 是真命题 (B)
是真命题 (B)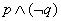 是真命题
是真命题 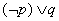 是真命题 (D)
是真命题 (D) 是假命题
是假命题 的参数方程为
的参数方程为
 为参数
为参数 ,则圆
,则圆 的距离为______.
的距离为______.  满足
满足 ,且当
,且当 时,
时, ,则当
,则当 时,
时, (B)
(B)  (C)
(C)  (D)
(D) 
 中,记不等式组
中,记不等式组 所表示的平面区域为
所表示的平面区域为 的作用下,区域
的作用下,区域 对应的象为点
对应的象为点 .
.  的作用下,点
的作用下,点 的原象是 ;
的原象是 ; :
: 与直线
与直线 :
: 垂直,那么
垂直,那么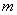 的值为
的值为 B.
B. C.
C. D.
D.
 中,如果
中,如果  ,
, ,
, ,那么
,那么 等于
等于  B.
B. C.
C. D.
D.
 在
在 上的最大值、最小值分别是
上的最大值、最小值分别是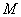 ,
,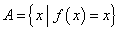 .
.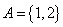 ,且
,且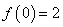 ,求
,求 ,且
,且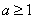 ,记
,记 ,求
,求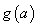 的最小值.
的最小值. .
. 时,求函数
时,求函数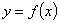 的图象在点
的图象在点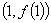 处的切线方程;
处的切线方程; 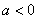 ,若函数
,若函数 的下方,求
的下方,求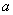 的取值范围;
的取值范围;