题目内容
已知函数 ,x∈R.
,x∈R.
(Ⅰ)求函数f(x)的最大值和最小值;
(Ⅱ)如图,函数f(x)在[﹣1,1]上的图象与x轴的交点从左到右分别为M、N,图象的最高点为P,求 与
与 的夹角的余弦.
的夹角的余弦.
 ,x∈R.
,x∈R.(Ⅰ)求函数f(x)的最大值和最小值;
(Ⅱ)如图,函数f(x)在[﹣1,1]上的图象与x轴的交点从左到右分别为M、N,图象的最高点为P,求
 与
与 的夹角的余弦.
的夹角的余弦.
解:(Ⅰ)∵ =
=
∵x∈R∴ ,
,
∴函数f(x)的最大值和最小值分别为1,﹣1.
(Ⅱ)解法1:令 得
得 ,
,
∵x∈[﹣1,1]∴ 或
或 ∴
∴ ,
,
由 ,且x∈[﹣1,1]得
,且x∈[﹣1,1]得 ∴
∴ ,
,
∴ ,
,
∴ =
= .
.
解法2:过点P作PA⊥x轴于A,则|PA|=1,
由三角函数的性质知 ,
,
 ,
,
由余弦定理得 =
= .
.
解法3:过点P作PA⊥x轴于A,则|PA|=1,
由三角函数的性质知 ,
,

在Rt△PAM中,
∵PA平分∠MPN∴cos∠MPN=cos2∠MPA=2cos2∠MPA﹣1= .
.
 =
=
∵x∈R∴
 ,
,∴函数f(x)的最大值和最小值分别为1,﹣1.
(Ⅱ)解法1:令
 得
得 ,
,∵x∈[﹣1,1]∴
 或
或 ∴
∴ ,
,由
 ,且x∈[﹣1,1]得
,且x∈[﹣1,1]得 ∴
∴ ,
,∴
 ,
,∴
 =
= .
.解法2:过点P作PA⊥x轴于A,则|PA|=1,
由三角函数的性质知
 ,
, ,
,由余弦定理得
 =
= .
.解法3:过点P作PA⊥x轴于A,则|PA|=1,
由三角函数的性质知
 ,
,
在Rt△PAM中,

∵PA平分∠MPN∴cos∠MPN=cos2∠MPA=2cos2∠MPA﹣1=
 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (x∈R).若
(x∈R).若 ,
, .求cos2x的值.
.求cos2x的值. ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.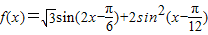 (x∈R).
(x∈R). ,x∈R
,x∈R
 ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.