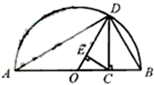
题目内容

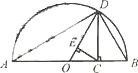精英家教网设a＞0，b＞0，称
2aba+b
为a，b的调和平均数．如图，C为线段AB上的点，且AC=a，CB=b，O为AB中点，以AB为直径做半圆．过点C作AB的垂线交半圆于D．连接OD，AD，BD．过点C作OD的垂线，垂足为E．则图中线段OD的长度是a，b的算术平均数，线段
 
的长度是a，b的几何平均数，线段
 
的长度是a，b的调和平均数．
分析：在直角三角形中，由DC为高，根据射影定理可得CD2=AC•CB，变形两边开方，得到CD长度为a，b的几何平均数；根据a，b与OC之间的关系，表示出OC的长度，根据直角三角形OCE和直角三角形CDE之间边的关系得到CE的长，得到OE进而ED，得到结果．
解答：解：在Rt△ADB中DC为高，则由射影定理可得CD2=AC•CB，
∴CD=
ab
，即CD长度为a，b的几何平均数，
将OC=a-
a+b
2
=
a-b
2
，CD=
ab
，OD=
a+b
2
代入OD•CE=OC•CD
可得CE=
a-b
a+b
ab

故OE=
OC2-CE2
=
(a-b)2
2(a+b)
，
∴ED=OD-OE=
2ab
a+b
，
∴DE的长度为a，b的调和平均数．
故选CD；DE
点评：本题是一个新定义问题，解题过程中主要应用直角三角形边之间的比例关系，得到比例式，本题是一个平面几何与代数中的平均数结合的问题，是一个综合题．
练习册系列答案
相关题目
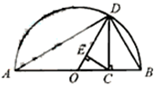设a＞0，b＞0，称
2aba+b
为a，b的调和平均数．如图，C为线段AB上的点，且AC=a，CB=b，O为AB中点，以AB为直径做半圆．过点C作AB的垂线交半圆于D．连接OD，AD，BD．过点C作OD的垂线，垂足为E．则图中线段OD的长度是a，b的算术平均数，线段CD的长度是a，b的几何平均数，那么a，b的调和平均数是线段
DE
DE
的长度．
若给定椭圆C：ax2+by2=1（a＞0，b＞0，a≠b）和点N（x0，y0），则称直线l：ax0x+by0y=1为椭圆C的“伴随直线”．
（1）若N（x0，y0）在椭圆C上，判断椭圆C与它的“伴随直线”的位置关系（当直线与椭圆的交点个数为0个、1个、2个时，分别称直线与椭圆相离、相切、相交），并说明理由；
（2）命题：“若点N（x0，y0）在椭圆C的外部，则直线l与椭圆C必相交．”写出这个命题的逆命题，判断此逆命题的真假，说明理由；
（3）若N（x0，y0）在椭圆C的内部，过N点任意作一条直线，交椭圆C于A、B，交l于M点（异于A、B），设
MA
=λ1
AN
，
MB
=λ2
BN
，问λ1+λ2是否为定值？说明理由．
设a＞0，b＞0，已知函数f（x）=．
（Ⅰ）当a≠b时，讨论函数f（x）的单调性；
（Ⅱ）当x＞0时，称f（x）为a、b关于x的加权平均数．
（i）判断f（1），f（），f（）是否成等比数列，并证明f（）≤f（）；
（ii）a、b的几何平均数记为G．称为a、b的调和平均数，记为H．若H≤f（x）≤G，求x的取值范围．
设a＞0，b＞0，称
2ab
a+b
为a，b的调和平均数．如图，C为线段AB上的点，且AC=a，CB=b，O为AB中点，以AB为直径做半圆．过点C作AB的垂线交半圆于D．连接OD，AD，BD．过点C作OD的垂线，垂足为E．则图中线段OD的长度是a，b的算术平均数，线段CD的长度是a，b的几何平均数，那么a，b的调和平均数是线段______的长度．
精英家教网

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网