题目内容
14.已知函数f(x)=$\left\{\begin{array}{l}{|lgx|,x>0}\\{-{x}^{2}-2x,x≤0}\end{array}\right.$,(1)分别求方程f(x)=1,方程f(x)=$\frac{1}{2}$的根的个数;
(2)试求关于x的函数y=2f2(x)-3f(x)+1的零点个数.
分析 (1)作函数f(x)=$\left\{\begin{array}{l}{|lgx|,x>0}\\{-{x}^{2}-2x,x≤0}\end{array}\right.$的图象,从而化方程的根的个数为函数的图象的交点的个数;
(2)令2f2(x)-3f(x)+1=0得f(x)=1或f(x)=$\frac{1}{2}$,从而解得.
解答 解:(1)作函数f(x)=$\left\{\begin{array}{l}{|lgx|,x>0}\\{-{x}^{2}-2x,x≤0}\end{array}\right.$的图象如下,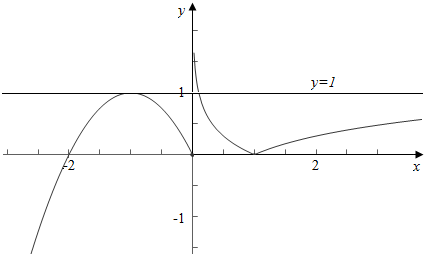 ,
,
结合图象可知,函数f(x)与y=1有三个不同的交点,
函数f(x)与y=$\frac{1}{2}$有四个不同的交点,
故方程f(x)=1有3个不同的根,方程f(x)=$\frac{1}{2}$有4个不同的根.
(2)令2f2(x)-3f(x)+1=0得,
f(x)=1或f(x)=$\frac{1}{2}$,
结合(1)知,方程2f2(x)-3f(x)+1=0有7个不同的根,
故关于x的函数y=2f2(x)-3f(x)+1的零点个数为7.
点评 本题考查了数形结合的思想应用及方程的根与函数的零点的关系应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.设数列{an}的通项公式为an=(-1)n(2n-1)•cos$\frac{nπ}{2}+1(n∈{N^*})$,其前n项和为Sn,则S120=( )
| A. | -60 | B. | -120 | C. | 180 | D. | 240 |
2.已知cos(π-θ)=3m(m<0),且cos($\frac{π}{2}$+θ)(1-2cos2$\frac{θ}{2}$)<0,则θ是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
6.已知数列{an}的通项满足a1=1,且an+1=an+n+2n,则an=( )
| A. | $\frac{n(n-1)}{2}$+2n-1-1 | B. | $\frac{n(n-1)}{2}$+2n-1 | C. | $\frac{n(n+1)}{2}$+2n-1-1 | D. | $\frac{n(n+1)}{2}$+2n-1 |
3.直角△ABC的三个顶点都在单位圆x2+y2=1上,点M($\frac{1}{2}$,$\frac{1}{2}$).则|$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$|最大值是( )
| A. | $\sqrt{2}+1$ | B. | $\sqrt{2}+2$ | C. | $\frac{3\sqrt{2}}{2}+1$ | D. | $\frac{3\sqrt{2}}{2}+2$ |
