题目内容
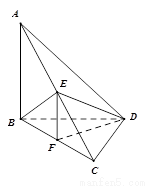
如图,已知三棱锥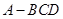 ,
,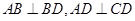 ,
,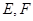 分别为
分别为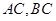 的中点,且
的中点,且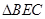 为正三角形.
为正三角形.
(Ⅰ)求证: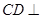 平面
平面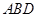 ;
;
(Ⅱ)若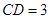 ,
,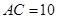 ,求点
,求点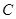 到平面
到平面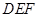 的距离.
的距离.
【答案】
(Ⅰ)如下证明(Ⅱ)
【解析】
试题分析:(Ⅰ)解:
 为正三角形,
为正三角形, 为
为 中点
中点
 ∥
∥ ,
, ,
,
又 ,
, 平面
平面
 ,又
,又
 平面
平面
(Ⅱ)设点 到平面
到平面 的距离为
的距离为
 ,
, ,在
,在 中,
中, 为
为 中点,
中点, ,
,






 点
点 到平面
到平面 的距离为
的距离为
考点:直线与平面垂直的判定定理;点到平面的距离
点评:直线与平面平行、垂直的判定定理是常考知识点,在证明时,需结合定理的条件写,不可凭自己的主观意识去写。另外,求点到平面的距离常结合几何体的体积来求。

练习册系列答案
相关题目
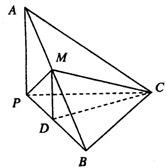 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形. 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
 (2013•鹰潭一模)如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
(2013•鹰潭一模)如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形. (2012•眉山二模)如图,已知三棱锥P-ABC中,PA⊥面ABC,AB⊥BC,PA=2,AB=BC=
(2012•眉山二模)如图,已知三棱锥P-ABC中,PA⊥面ABC,AB⊥BC,PA=2,AB=BC=