题目内容
 (2013•鹰潭一模)如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
(2013•鹰潭一模)如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.(I)求证:BC⊥平面APC;
(Ⅱ)若BC=3,AB=1O,求点B到平面DCM的距离.
分析:(I)根据正三角形三线合一,可得MD⊥PB,利用三角形中位线定理及空间直线夹角的定义可得AP⊥PB,由线面垂直的判定定理可得AP⊥平面PBC,即AP⊥BC,再由AC⊥BC结合线面垂直的判定定理可得BC⊥平面APC;
(Ⅱ)记点B到平面MDC的距离为h,则有VM-BCD=VB-MDC.分别求出MD长,及△BCD和△MDC面积,利用等积法可得答案.
(Ⅱ)记点B到平面MDC的距离为h,则有VM-BCD=VB-MDC.分别求出MD长,及△BCD和△MDC面积,利用等积法可得答案.
解答: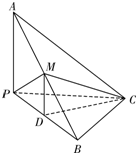 证明:(Ⅰ)如图,
证明:(Ⅰ)如图,
∵△PMB为正三角形,
且D为PB的中点,
∴MD⊥PB.
又∵M为AB的中点,D为PB的中点,
∴MD∥AP,
∴AP⊥PB.
又已知AP⊥PC,PB∩PC=P,PB,PC?平面PBC
∴AP⊥平面PBC,
∴AP⊥BC,
又∵AC⊥BC,AC∩AP=A,
∴BC⊥平面APC,…(6分)
解:(Ⅱ)记点B到平面MDC的距离为h,则有VM-BCD=VB-MDC.
∵AB=10,
∴MB=PB=5,
又BC=3,BC⊥PC,
∴PC=4,
∴S△BDC=
S△PBC=
PC•BC=3.
又MD=
,
∴VM-BCD=
MD•S△BDC=
.
在△PBC中,CD=
PB=
,
又∵MD⊥DC,
∴S△MDC=
MD•DC=
,
∴VB-MDC=
h•S△MDC=
•h•
=
∴h=
即点B到平面DCM的距离为
. …(12分)
 证明:(Ⅰ)如图,
证明:(Ⅰ)如图,∵△PMB为正三角形,
且D为PB的中点,
∴MD⊥PB.
又∵M为AB的中点,D为PB的中点,
∴MD∥AP,
∴AP⊥PB.
又已知AP⊥PC,PB∩PC=P,PB,PC?平面PBC
∴AP⊥平面PBC,
∴AP⊥BC,
又∵AC⊥BC,AC∩AP=A,
∴BC⊥平面APC,…(6分)
解:(Ⅱ)记点B到平面MDC的距离为h,则有VM-BCD=VB-MDC.
∵AB=10,
∴MB=PB=5,
又BC=3,BC⊥PC,
∴PC=4,
∴S△BDC=
| 1 |
| 2 |
| 1 |
| 4 |
又MD=
5
| ||
| 2 |
∴VM-BCD=
| 1 |
| 3 |
5
| ||
| 2 |
在△PBC中,CD=
| 1 |
| 2 |
| 5 |
| 2 |
又∵MD⊥DC,
∴S△MDC=
| 1 |
| 2 |
| 25 |
| 8 |
| 3 |
∴VB-MDC=
| 1 |
| 3 |
| 1 |
| 3 |
| 25 |
| 8 |
| 3 |
5
| ||
| 2 |
∴h=
| 12 |
| 5 |
即点B到平面DCM的距离为
| 12 |
| 5 |
点评:本题考查的知识点是直线与平面垂直的判定,点到平面的距离,其中(1)的关键是熟练掌握空间线线垂直与线面垂直之间的相互转化,(2)的关键是等积法的使用.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目