题目内容
如图,已知点 ,正方形
,正方形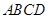 内接于⊙
内接于⊙ ,
, 、
、 分别为边
分别为边 、
、 的中点,当正方形
的中点,当正方形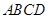 绕圆心
绕圆心 旋转时,
旋转时, 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
C
解析试题分析:由题意 ,
, ,则
,则
 ,由于
,由于 ,
, ,所以
,所以 的最大值为2,最小值为
的最大值为2,最小值为 ,即
,即
 .
.
也可以这样做, 且长度为1,可设
且长度为1,可设 ,
, ,然后用坐标求解.答案选
,然后用坐标求解.答案选 .
.
考点:向量的线性表示,与向量的数量积及其性质.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
设 ,
, ,
,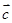 为同一平面内具有相同起点的任意三个非零向量,且满足
为同一平面内具有相同起点的任意三个非零向量,且满足 与
与 不共线,
不共线, ⊥
⊥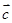 ,|
,| |=|
|=|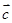 |,则
|,则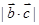 的值一定等于( )
的值一定等于( )
A.以 , , 为两边的三角形的面积 为两边的三角形的面积 |
B.以 , ,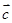 为两边的三角形的面积 为两边的三角形的面积 |
C.以 , , 为邻边的平行四边形的面积 为邻边的平行四边形的面积 |
D.以 , ,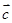 为邻边的平行四边形的面积 为邻边的平行四边形的面积 |
如图,在△ABC中,AB=3,AC=5,若O为△ABC的外心,则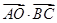 的值是(( )
的值是(( )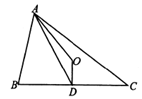
A.4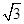 | B.8 | C.6 | D.6 |
已知三点A(1,1)、B(-1,0)、C(3,-1),则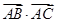 等于( )
等于( )
| A.-2 | B.-6 | C.2 | D.3 |
如图,在 中,
中, ,
,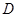 是
是 边上一点,
边上一点, ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
若两非零向量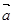 与
与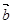 的夹角为
的夹角为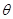 ,定义向量运算
,定义向量运算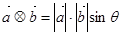 ,已知向量
,已知向量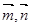 满足
满足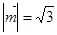 ,
,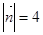 ,
,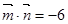 ,则
,则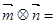 ( )
( )
| A.2 | B.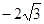 | C. | D.3 |
给出下列结论:①若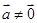 ,
,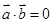 ,则
,则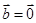 ; ②若
; ②若 ,则
,则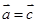 ;
;
③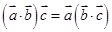 ; ④
; ④ ;⑤若
;⑤若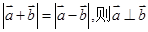
其中正确的为( )
| A.②③④ | B.①②⑤ | C.④⑤ | D.③④⑤ |
已知向量a、b的夹角为120°,且|a|=|b|=4,那么b·(2a+b)的值为( )
| A.48 | B.32 | C.1 | D.0 |
 =
= ,
, =(1-λ)
=(1-λ) ,λ∈R,若
,λ∈R,若 ·
· =-
=- ,则
,则 =( )
=( )


