题目内容
如图,α-l-β是120°的二面角,A、B是棱l上的两点,且AB=2,D在平面α内,三角形ABD是等腰直角三角形,∠DAB=90°,C在平面β内,三角形ABC是直角三角形,∠ACB=90°,∠ABC=60°.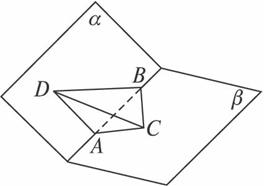
(1)求三棱锥D-ABC的体积;
(2)求直线BD与平面β所成的角的正弦值;
(3)求二面角D-AC-B的平面角的正切值.
解:(1)过D作平面β的垂线,垂足为O,连结OA并延长至E.
∵AB⊥AD,OA为DA在平面β内的射影,
∴OA⊥AB,∴∠DAE为二面角α-l-β的平面角,∴∠DAE=120°,
∴∠DAO=60°,∴AD=AB=2,∴DO=![]() .
.
又D到平面β的距离DO=![]() ,
,
∴VABC=![]() ·SABC·DO=
·SABC·DO=![]() .
.
(2)由(1)知∠DBO为BD与平面β成的角,
∴sin∠DBO=![]() .
.
(3)过O在β内作OF⊥AC,交AC的反向延长线于F,连结DF,则AC⊥DF,
∴∠DFO为二面角DACB的平面角,
又在三角形DOA中,OA=2cos60°=1,即∠OAF=∠EOC=60°,
∴OF=1·sin60°=![]() ,∴tan∠DFO=
,∴tan∠DFO=![]() =2.
=2.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
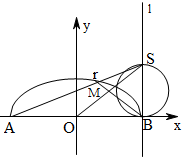 已知A,B 分别为曲线C:
已知A,B 分别为曲线C:
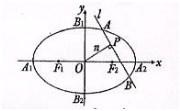 如图,椭圆C2
如图,椭圆C2 如图,椭圆
如图,椭圆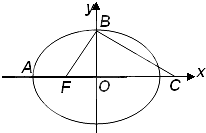 (2009•泰安一模)如图,点F是椭圆
(2009•泰安一模)如图,点F是椭圆