题目内容
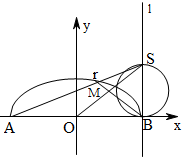 已知A,B 分别为曲线C:
已知A,B 分别为曲线C:| x2 |
| a2 |
(1)若曲线C为半圆,点T为圆弧
 |
| AB |
(2)如图,点M是以SB为直径的圆与线段TB的交点,试问:是否存在a,使得O,M,S三点共线?若存在,求出a的值,若不存在,请说明理由.
分析:(1)先由曲线C为半圆时得到a=1,再由点T为圆弧
的三等分点得∠BOT=60°或120°,再对每一种情况下利用解三角的方法分别求点S的坐标即可;
(II)先把直线AS的方程与曲线方程联立,求出点T的坐标以及kBT,进而求得kSM;以及直线SM的方程,再利用O在直线SM上即可求出a的值.
 |
| AB |
(II)先把直线AS的方程与曲线方程联立,求出点T的坐标以及kBT,进而求得kSM;以及直线SM的方程,再利用O在直线SM上即可求出a的值.
解答:解:(Ⅰ)当曲线C为半圆时,a=1,
由点T为圆弧
的三等分点得∠BOT=60°或120°.┉┉(1分)
(1)当∠BOT=60°时,∠SAB=30°.
又AB=2,故在△SAE中,有SB=AB•tan30°=
,∴s(1,
);┉┉(3分)
(2)当∠BOT=120°时,同理可求得点S的坐标为(1,2
),
综上,s(1,
)或s(1,2
).┉┉(5分)
(Ⅱ)假设存在a,使得O,M,S三点共线.
由于点M在以SB为直径的圆上,故SM⊥BT.
显然,直线AS的斜率k存在且K>0,可设直线AS的方程为y=k(x+a)
由
?(1+a2k2)x2+2a3k2x+a4k2-a2=0.
设点T(xT,yT),则有xT• (-a)=
,
故xT=
?yT=k(xT+a )=
,故T(
,
)
又B(a,0)∴kBT=
=-
,kSM=a2k.
由
?S(a,2ak),所直线SM的方程为y-2ak=a2k(x-a)
O,S,M三点共线当且仅当O在直线SM上,即2ak=a2ka.
又a>0,k>0?a=
,
故存在a=
,使得O,M,S三点共线.
由点T为圆弧
 |
| AB |
(1)当∠BOT=60°时,∠SAB=30°.
又AB=2,故在△SAE中,有SB=AB•tan30°=
2
| ||
| 3 |
2
| ||
| 3 |
(2)当∠BOT=120°时,同理可求得点S的坐标为(1,2
| 3 |
综上,s(1,
2
| ||
| 3 |
| 3 |
(Ⅱ)假设存在a,使得O,M,S三点共线.
由于点M在以SB为直径的圆上,故SM⊥BT.
显然,直线AS的斜率k存在且K>0,可设直线AS的方程为y=k(x+a)
由
|
设点T(xT,yT),则有xT• (-a)=
| a4k2-a2 |
| 1+a2k2 |
故xT=
| a-a3k2 |
| 1+a2k2 |
| 2ak |
| 1+a2k2 |
| a-a3k2 |
| 1+a2k2 |
| 2ak |
| 1+a2k2 |
又B(a,0)∴kBT=
| yT |
| xT-a |
| 1 |
| a2k |
由
|
O,S,M三点共线当且仅当O在直线SM上,即2ak=a2ka.
又a>0,k>0?a=
| 2 |
故存在a=
| 2 |
点评:本题主要考查直线和圆相切,直线的方程,三点共线和圆的几何性质等基础知识,考查用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查解决问题的能力和运算能力.

练习册系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( ) 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )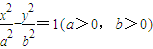 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若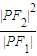 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )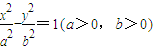 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若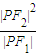 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )